
 Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 38°, 78° и 64°.
Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 38°, 78° и 64°.
Пусть:
∠KMP=38°
∠MKP=78°
∠KPM=64°
Рассмотрим треугольник AMK.
AM=AK (по
второму свойству касательной)
Следовательно треугольник AMK -
равнобедренный, тогда, по
свойству равнобедренного треугольника:
∠AMK=∠AKM
Заметим, что оба этих угла охватывают дугу MK, и следовательно равны половине ее градусной меры (по
свойству углов на окружности).
∠MPK является
вписанным в окружность углом и опирается на эту же дугу, следовательно и он равен половине градусной меры этой дуги.
Получается, что:
∠AMK=∠AKM=∠MPK=64°
Применив
теорему о сумме углов треугольника:
180°=∠AMK+∠AKM+∠MAK
180°=64°+64°+∠MAK
∠MAK=52°
Аналогично, для двух других треугольников получим:
∠BKP=∠BPK=∠PMK=38°
∠KBP=180°-38°-38°=104°
И...
∠CPM=∠CMP=∠MKP=78°
∠PCM=180°-78°-78°=24°
Ответ: 52°, 104° и 24°
Поделитесь решением
Присоединяйтесь к нам...
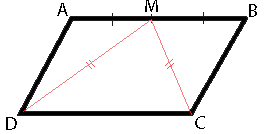 В параллелограмме ABCD точка M — середина стороны AB. Известно, что MC=MD. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме ABCD точка M — середина стороны AB. Известно, что MC=MD. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AOD.
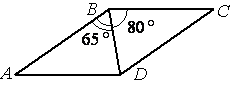 Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 80°. Найдите меньший угол параллелограмма.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 80°. Найдите меньший угол параллелограмма.
 Площадь прямоугольного треугольника равна 2450√
Площадь прямоугольного треугольника равна 2450√
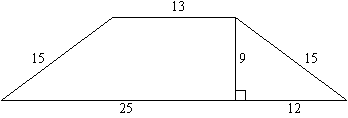 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Комментарии:
(2015-05-26 20:54:35) : Благодарю!
(2015-05-20 08:06:59) Администратор: Киса, угол можно обозначать по разному, поэтому ∠PMK и ∠KMP - это одно и тоже.
(2015-05-20 00:39:11) Киса: А почему у вас ∠BKP=∠BPK=∠PMK=38° вить вы писали, что ∠KMP=38°?