Автор: страдалец
В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=16, BC=15.
По условию задачи AB перпендикулярна BC, следовательно перпендикулярна и AD (т.к. в
трапеции основания параллельны).
Расстояние от точки Е до прямой CD - отрезок, перпендикулярный CD и проходящий через точку Е.
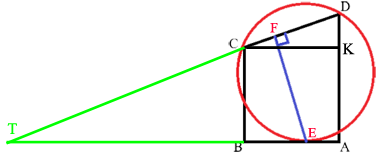Продолжим стороны AB и CD до пересечения в точке T.
Проведем CK параллельно AB.
AK=BС (т.к. ABKC -
прямоугольник).
KD=AD-AK=16-15=1
По
определению косинуса: cos∠CDK=KD/CD=1/CD
Рассмотрим треугольники TCB и CKD.
∠CTB=∠DCK (т.к. это
соответственные углы при параллельных прямых TA и CK)
∠TBC=∠CKD=90°
Следовательно, эти треугольники
подобны (по
первому признаку подобия).
Тогда, BC/KD=TC/CD
15/1=TC/CD
TC=15CD
По
теореме о касательно и секущей:
TE2=TD*TC=(TC+CD)*TC=(15CD+CD)15CD=16CD*15CD=240CD2
TE=CD√
Рассмотрим треугольники TEF и TAD.
∠CTB - общий
∠EFT=∠TAD=90°
Следовательно, применив
теорему о сумме углов треугольника, получаем, что ∠TEF=∠ADT.
Следовательно, cos∠TEF=cos∠ADT.
EF=TE*cos∠TEF=TE*cos∠ADT
Так как ∠ADT и ∠CDK это один и тот же угол, то подставляем ранее найденное значение cos∠CDK=1/CD.
EF=TE/CD=4CD√
Ответ: EF=4√
Поделитесь решением
Присоединяйтесь к нам...
Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
В трапеции ABCD AB=CD, ∠BDA=49° и ∠BDC=13°. Найдите угол ABD. Ответ дайте в градусах.
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 36 и 39.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=60°. Найдите угол NMB. Ответ дайте в градусах.
Стороны AC, AB, BC треугольника ABC равны 3√
Хочу получать новые решения
Ни какого спама
Комментарии:
(2017-03-17 02:08:01) Администратор: Карина, я добавил в решение пару строк, чтобы стало понятней.
(2017-03-16 11:04:30) Карина: Подскажите, пожалуйста, как получилось что TE*cos∠ADT=TE/CD?
(2017-02-20 21:18:33) Администратор: Марина, по теореме о касательной и секущей. Нажимайте на ссылки в тексте решения, будут показываться теоремы и определения, на которые я ссылаюсь при решении.
(2017-02-20 21:16:10) Марина: Скажите пожалуйста, почему TE2=TD*TC=(TC+CD)*ТС?
(2014-05-26 09:35:48) Администратор: Настя, по первому комментарию: указанные треугольники, конечно, подобны, но для решения подобие нам не интересно. Два угла одно треугольника равны двум углам другого треугольника, поэтому мы и применяем теорему о сумме углов треугольника, не используя подобие.
(2014-05-26 00:11:37) Настя: Спасибо большое за решение,оно мне очень помогло. Но есть один нюанс: треугольники TEF и TAD подобны по 2-м углам (как вы и указали), а потом уже по теореме о сумме углов треугольника получаем,что ∠TEF=∠ADT.