Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 7:6, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 48.
Пусть AD -
биссектриса, описанная в условии.
BC - сторона, равная 48.
Рассмотрим треугольник ADC.
Для этого треугольника CO -
биссектриса,
По
свойству биссектрисы:
AO/OD=AC/CD=7/6
6*AC=7*CD
Рассмотрим треугольник ABD.
Для этого треугольника BO -
биссектриса,
По
свойству биссектрисы:
AO/OD=AB/BD=7/6
6*AB=7*BD
Складываем полученные равенства:
6*AC+6*AB=7*CD+7*BD
6(AC+AB)=7(CD+BD), CD+BD=BC=48
6(AC+AB)=7*48
AC+AB=56
PABC=AC+AB+BC=56+48=104
Ответ: PABC=104
Поделитесь решением
Присоединяйтесь к нам...
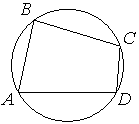Угол A четырёхугольника ABCD, вписанного в окружность, равен 82°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.
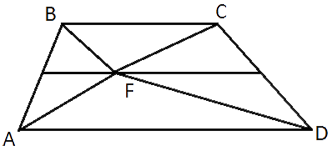На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
Медиана BM треугольника ABC равна 3 и является диаметром окружности, пересекающей сторону BC в её середине. Найдите диаметр описанной окружности треугольника ABC.
Радиус окружности, вписанной в трапецию, равен 24. Найдите высоту этой трапеции.
Синус острого угла A треугольника ABC равен 
. Найдите CosA.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2014-05-29 16:49:51) Администратор: Алла, так в сущности задача так и решена, просто решение расписано для понимания.
(2014-05-29 16:00:51) Алла: Каждая биссектриса треугольника делится в точке пересечение с биссектрисами в отношений суммы прилежащих сторон к противолежащей,считая от вершины. Тоесть по условию СО/OD=7/6=(AB+AC)/BC .Подставляя все значения будет 7/6=(AB+AC)/48. AB+AC=56,P ABC= AB+AC+BC=56+48=104.Мне кажется это решение будет короче и легче)