Боковая сторона равнобедренного треугольника равна 10, а основание равно 12. Найдите площадь этого треугольника.
Площадь треугольника равна a*h/2, где h -
высота треугольника, а - сторона треугольника, к которой проведена высота.
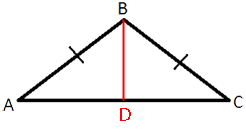
SABC=AC*BD/2
AD=DC=AC/2=12/2=6 (по
свойству равнобедренного треугольника высота является
медианой)
Тогда, по
теореме Пифагора:
AB2=BD2+AD2
102=BD2+62
100=BD2+36
BD2=64
BD=8
SABC=AC*BD/2=12*8/2=48
Ответ: SABC=48
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 8. Найдите площадь четырёхугольника ABMN.
Найдите площадь трапеции, изображённой на рисунке.
Основания трапеции равны 3 и 9, а высота равна 5. Найдите среднюю линию этой трапеции.
Какие из следующих утверждений верны?
1) Площадь треугольника меньше произведения двух его сторон.
2) Средняя линия трапеции равна сумме её оснований.
3) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 9 и 5. Найдите площадь параллелограмма ABCD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2022-05-12 09:27:42) : квадрат со стороной 8 см описан около окружности. найдите площадь прямоугольного треугольника с острым углом 30, вписанного в данную окружность
(2014-05-17 14:33:39) Администратор: Танюшка, спасибо, хорошее логичное решение. Опубликуем в скором времени.
(2014-05-17 14:29:36) танюшка: Можно решить через теорему Герона. Боковые стороны равны между собой и равны 10.Находим полупериметр: р=(10+10+12)/2=16.Подставляем данные в формулу: S=√16(16-10)*(16-10)*(16-12); S=√64*36 ; S=8*6=48