
 Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=5, AC=45.
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=5, AC=45.
Рассмотрим треугольники ABC и ABH.
∠A - общий
∠AHB=∠ABC
Следовательно, эти треугольники
подобны (по
признаку подобия)
Тогда AC/AB=AB/AH (гипотенуза большого треугольника относится к гипотенузе маленького как малый катет большого треугольника к малому катету маленького треугольника)
45/AB=AB/5
45*5=AB2
225=AB2
AB=15
Ответ: AB=15
Поделитесь решением
Присоединяйтесь к нам...
 Основания трапеции относятся как 2:3. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции?
Основания трапеции относятся как 2:3. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции?
 В треугольнике ABC угол C прямой, BC=2, cosB=0,4. Найдите AB.
В треугольнике ABC угол C прямой, BC=2, cosB=0,4. Найдите AB.
Стороны AC, AB, BC треугольника ABC равны 2√
 Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 60, тангенс угла BAC равен 5/12. Найдите радиус окружности, вписанной в треугольник ABC.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 60, тангенс угла BAC равен 5/12. Найдите радиус окружности, вписанной в треугольник ABC.
Косинус острого угла A треугольника ABC равен 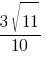 . Найдите sinA.
. Найдите sinA.
Комментарии: