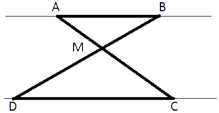Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=16, DC=24, AC=25.
Рассмотрим треугольники ABM и CDM.
∠AMB=∠CMD (т.к. они
вертикальные).
∠ABM=∠CDM (т.к. они
накрест-лежащие).
Следовательно, треугольники ABM и CDM
подобны (по
первому признаку подобия).
AC=AM+MC => AM=AC-MC
Тогда:
AB/CD=AM/MC
16/24=(AC-MC)/MC
16MC=24(25-MC)
2MC=3(25-MC)
2MC=75-3MC
5MC=75
MC=15
Ответ: MC=15
Поделитесь решением
Присоединяйтесь к нам...
Прямая, параллельная стороне
AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=3:7, KM=12.
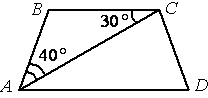Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
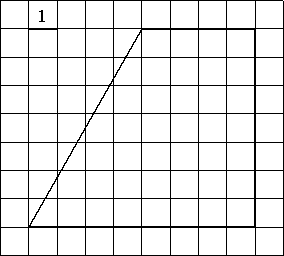Найдите площадь трапеции, изображённой на рисунке.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 96. Найдите стороны треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: