Площадь прямоугольного треугольника равна
722√
Обозначим:
a - искомый катет
b - второй катет
c - гипотенуза
sin30°=1/2 (
табличное значение)
sin30°=a/c=1/2 (по
определению синуса)
c=2a
По
теореме Пифагора:
a2+b2=c2
a2+b2=(2a)2
b2=3a2
b=a√
Из условия: Sтреугольника=ab/2=722√
a*a√
Сокращаем √
a2=722*2=1444
a=38
Ответ: a=38
Поделитесь решением
Присоединяйтесь к нам...
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 120°, а CD=34.
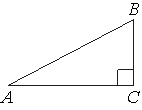В треугольнике ABC угол C равен 90°, tgB=7/6, BC=18. Найдите AC.
Стороны AC, AB, BC треугольника ABC равны 2√
Прямая, параллельная стороне
AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=3:4, KM=18.
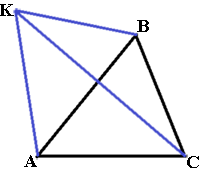
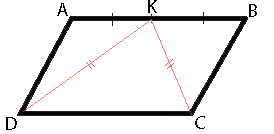В параллелограмме ABCD точка K — середина стороны AB. Известно, что KC = KD. Докажите, что данный параллелограмм — прямоугольник.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-04 15:53:49) Александр: Аа, точно. a^2+b^2=(2a)^2 то есть a^2+b^2=4a^2 и дальше b^2=-a^2+4a^2
(2015-05-04 15:50:57) Администратор: Александр, Вы ошибаетесь:
a2+b2=(2a)2
a2+b2=4a2
b2=4a2-a2
b2=3a2
(2015-05-04 15:46:26) Александр: Почему b^2+a^2=(2a)^2 и при переносе вы получаете b^2=3a^2 Вы должны поменять знак при переносе и получить b^2=-a^2+2a^2