
 Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=18, а сторона BC в 1,2 раза меньше стороны AB.
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=18, а сторона BC в 1,2 раза меньше стороны AB.
Рассмотрим четырехугольник PKBC.
PKBC вписан в окружность, следовательно выполняется условие: сумма противоположных углов четырехугольника равна 180° (условие того, что четырехугольник можно вписать в окружность).
Т.е. ∠PKB+∠BCP=180°
∠PKB+∠AKP=180° (т.к. это
смежные углы).
Следовательно, ∠AKP=∠BCP
Рассмотрим треугольники ABC и AKP.
∠AKP=∠BCP (это мы выяснили чуть выше)
∠A - общий, тогда эти треугольники
подобны (по
признаку подобия).
Следовательно, KP/BC=AK/AC=AP/AB (из
определения подобных треугольников).
Нас интересует равенство KP/BC=AP/AB
KP/BC=18/(1,2BC)
KP=18BC/(1,2BC)=15
Ответ: KP=15
Поделитесь решением
Присоединяйтесь к нам...
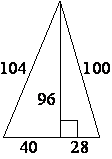 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
 В трапеции ABCD AB=CD, ∠BDA=10° и ∠BDC=109°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, ∠BDA=10° и ∠BDC=109°. Найдите угол ABD. Ответ дайте в градусах.
 На отрезке AB выбрана точка C так, что AC=12 и BC=3. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
На отрезке AB выбрана точка C так, что AC=12 и BC=3. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
 В треугольнике ABC сторона AB=32, AC=64, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.
В треугольнике ABC сторона AB=32, AC=64, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.
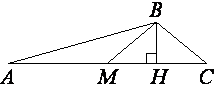 В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=64, HC=16 и ∠ACB=37°. Найдите угол AMB. Ответ дайте в градусах.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=64, HC=16 и ∠ACB=37°. Найдите угол AMB. Ответ дайте в градусах.
Комментарии:
(2018-12-10 12:56:43) Администратор: Анна, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2018-12-09 13:20:49) Анна : Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=9, а сторона BC в 3 раза меньше стороны AB
(2017-05-02 23:00:29) Администратор: Инокентий, я проверил решение, все правильно. А в чем у Вас сомнения?
(2017-05-02 17:52:44) инокентий: вы уверены в правильности задачи?