
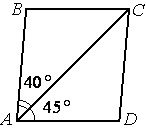 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 40°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 45° и 40°. Найдите больший угол параллелограмма.
По
свойству
параллелограмма /A=/C=45°+40°=85° и /B=/D.
Найдем углы B и D.
Стороны AD и BC параллельны (по
определению параллелограмма). Если рассмотреть AC как секущую к этим параллельным прямым, то становится очевидным, что /DAC=/BCA=45° (т.к. они
накрест лежащие).
Рассмотрим треугольник ABC.
По
теореме о сумме углов треугольника мы можем написать: 180°=/CAB+/B+/BCA
180°=40°+/B+45°
/B=95°=/D
95>85, следовательно углы B и D - бОльшие.
Ответ: больший угол равен 95°.
Поделитесь решением
Присоединяйтесь к нам...
Площадь прямоугольного треугольника равна 392√
 В равнобедренную трапецию, периметр которой равен 200, а площадь равна 2000, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
В равнобедренную трапецию, периметр которой равен 200, а площадь равна 2000, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
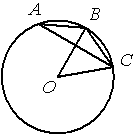 Точка О – центр окружности, /BOC=50° (см. рисунок). Найдите величину угла BAC (в градусах).
Точка О – центр окружности, /BOC=50° (см. рисунок). Найдите величину угла BAC (в градусах).
 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
 Боковые стороны AB и CD трапеции ABCD равны соответственно 18 и 30, а основание BC равно 3. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Боковые стороны AB и CD трапеции ABCD равны соответственно 18 и 30, а основание BC равно 3. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Комментарии:
(2020-11-10 17:40:54) ПУк: В четырехугольнике ABCD ABǁ CD, BCǁ AD, AC=16см, BD=20см, AB=15см. Найдите периметр треугольника COD.