
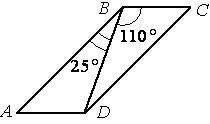 Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
25° и 110°. Найдите меньший угол параллелограмма.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
25° и 110°. Найдите меньший угол параллелограмма.
По
свойству
параллелограмма /B=/D=25°+110°=135° и /A=/C.
Найдем углы A и C.
Стороны AD и BC параллельны (по
определению параллелограмма). Если рассмотреть BD как секущую к этим параллельным прямым, то становится очевидным, что /CBD=/ADB=110° (т.к. они
накрест лежащие).
Рассмотрим треугольник ABD.
По
теореме о сумме углов треугольника мы можем написать: 180°=/ABD+/BDA+/A
180°=25°+110°+/A
/A=45°=/C
135>45, следовательно углы A и C - меньшие.
Ответ: меньший угол равен 45°.
Поделитесь решением
Присоединяйтесь к нам...
 Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
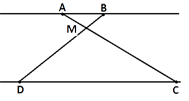 Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=15, DC=30, AC=39.
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=15, DC=30, AC=39.
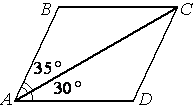 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите больший угол параллелограмма.
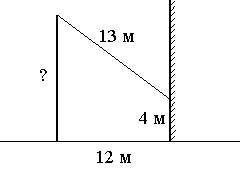 От столба к дому натянут провод длиной 13 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
От столба к дому натянут провод длиной 13 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
Укажите номера верных утверждений.
1) Любой квадрат является ромбом.
2) Против равных сторон треугольника лежат равные углы.
3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
Комментарии: