
 Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 5 см, тангенс угла ABC равен 2,4. Найдите радиус вписанной окружности треугольника ABC.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 5 см, тангенс угла ABC равен 2,4. Найдите радиус вписанной окружности треугольника ABC.
Радиус вписанной окружности можно вычислить по формуле R=(AC+CB-AB)/2. Для этого необходимо вычислить длины всех сторон данного треугольника.
Рассмотрим треугольник ABC.
По
определению tgABC=AC/CB=2,4 => AC=2,4*CB.
По
теореме Пифагора AB2=AC2+CB2
AB2=(2,4*CB)2+CB2
AB2=(CB/2,4)2+(2,4*CB/2,4)2
AB2=5,76*CB2+CB2
AB2=6,76*CB2
AB=2,6*CB
Необходимо вычислить CB.
Рассмотрим треугольник BCP.
По
определению tgABC=CP/BP=2,4 => CP=2,4*BP
По
теореме Пифагора CB2=CP2+BP2
CB2=(2,4*BP)2+BP2
CB2=6,76*BP2
CB=2,6*BP
BP=CB/2,6
r=(BP+CP-CB)/2
2*r=BP+2,4*BP-2,6*BP
2*5=0,8*BP
BP=12,5
CB=2,6*BP=2,6*12,5=32,5
Вычислив CB, мы можем вычислить AB и AC, указанные выше:
AB=2,6*CB=2,6*32,5=84,5
AC=2,4*CB=2,4*32,5=78
R=(AC+CB-AB)/2, тогда получаем:
R=(78+32,5-84,5)/2=13.
Ответ: R=13.
Поделитесь решением
Присоединяйтесь к нам...
 Площадь параллелограмма ABCD равна 176. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
Площадь параллелограмма ABCD равна 176. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
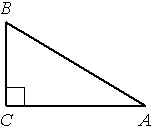 В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB.
В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB.
Какие из данных утверждений верны? Запишите их номера.
1) Вокруг любого треугольника можно описать окружность.
2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
3) Площадь трапеции равна произведению средней линии на высоту.
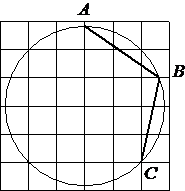 Найдите угол ABC . Ответ дайте в градусах.
Найдите угол ABC . Ответ дайте в градусах.
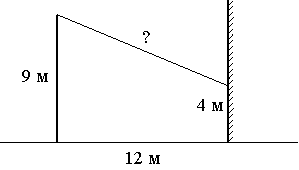 От столба высотой 9 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 12 м. Вычислите длину провода.
От столба высотой 9 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 12 м. Вычислите длину провода.
Комментарии: