
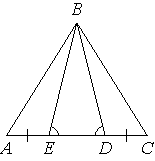
 На стороне АС треугольника АВС выбраны точки D и E так, что углы АDB и BEC равны (см. рисунок). Оказалось, что отрезки AЕ и CD тоже равны. Докажите, что треугольник АВС — равнобедренный.
На стороне АС треугольника АВС выбраны точки D и E так, что углы АDB и BEC равны (см. рисунок). Оказалось, что отрезки AЕ и CD тоже равны. Докажите, что треугольник АВС — равнобедренный.
1) По условию задачи /BED=/EDB, следовательно треугольник BDE - равнобедренный (по
свойству). По
определению равнобедренного треугольника BE=BD.
Смежные углы для /BED и /EDB тоже равны, /BDC=/BEA.
2) Рассмотрим треугольники ABE и CBD.
AE=CD (по условию),
BE=BD (согласно п.1),
/AEB=/CDB (из п.1),
следовательно эти треугольники равны (по
первому признаку равенства треугольников), а это значит, что BA=BC. Следовательно треугольник ABC - равнобедренный (по
определению).
Поделитесь решением
Присоединяйтесь к нам...
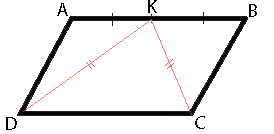 В параллелограмме ABCD точка K — середина стороны AB. Известно, что KC = KD. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме ABCD точка K — середина стороны AB. Известно, что KC = KD. Докажите, что данный параллелограмм — прямоугольник.
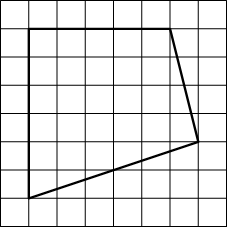 Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.
Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.
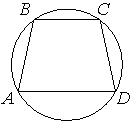 Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 31°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 31°. Найдите угол B этой трапеции. Ответ дайте в градусах.
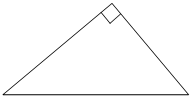 Один из острых углов прямоугольного треугольника равен 48°. Найдите его другой острый угол. Ответ дайте в градусах.
Один из острых углов прямоугольного треугольника равен 48°. Найдите его другой острый угол. Ответ дайте в градусах.
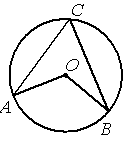 Точка О – центр окружности, /ACB=65° (см. рисунок). Найдите величину угла AOB (в градусах).
Точка О – центр окружности, /ACB=65° (см. рисунок). Найдите величину угла AOB (в градусах).
Комментарии: