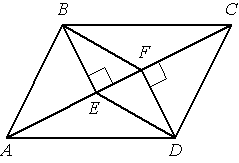
В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DЕ параллельны.
1) Рассмотрим треугольники ABE и CDF.
AB=CD (по
свойству параллелограмма).
/BAE=/DCF (т.к. это
внутренние накрест-лежащие углы для параллельных BC и AD и секущей AC).
/BEA=/DFC (т.к. оба эти угла прямые по условию).
Если два угла у данных треугольников попарно равны, то и третьи углы равны (по
теореме о сумме углов треугольника).
Следовательно треугольники ABE и CDF равны (по
второму признаку равенства треугольников). Отсюда следует, что BE=FD
2) Рассмотрим треугольники BFE и DEF.
BE=FD (из пункта 1), EF-общая сторона, /BEF=/DFE (т.к. это прямые углы по условию).
Следовательно треугольники BFE и DEF равны (по
первому признаку равенства треугольников). Отсюда следует, что BF=ED.
3) В итоге получаем, BF=ED и BE=FD, следовательно ВFDЕ —
параллелограмм (по
свойству параллелограмма).
Следовательно, ВF и DЕ параллельны (по
определению).
Поделитесь решением
Присоединяйтесь к нам...
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
Радиус окружности, описанной около квадрата, равен 48√2. Найдите радиус окружности, вписанной в этот квадрат.
В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
Картинка имеет форму прямоугольника со сторонами 24 см и 37 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1440 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.
Основание AC равнобедренного треугольника ABC равно 4. Окружность радиуса 2,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: