
 В треугольнике ABC угол C прямой, BC=3, cosB=0,6. Найдите AB.
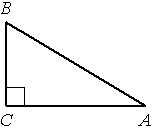
В треугольнике ABC угол C прямой, BC=3, cosB=0,6. Найдите AB.
По
определению косинуса cosB=BC/AB => AB=BC/cosB=3/0,6=5.
Ответ: AB=5.
Поделитесь решением
Присоединяйтесь к нам...
 Четырёхугольник ABCD со сторонами AB=19 и CD=22 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
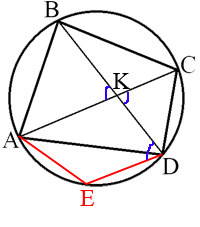
Четырёхугольник ABCD со сторонами AB=19 и CD=22 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
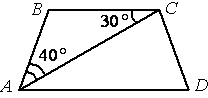 Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
 Радиус окружности, вписанной в равносторонний треугольник, равен 5. Найдите высоту этого треугольника.
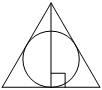
Радиус окружности, вписанной в равносторонний треугольник, равен 5. Найдите высоту этого треугольника.
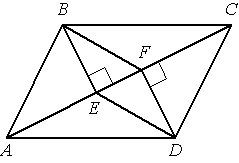 В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что треугольники BEF и DFE равны.
В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что треугольники BEF и DFE равны.
На какой угол (в градусах) поворачивается минутная стрелка, пока часовая поворачивается на 12°?
Комментарии: