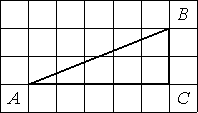
Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
По
определению тангенса: tgA=BC/AC=2/5=0,4.
Ответ: tgA=0,4.
Поделитесь решением
Присоединяйтесь к нам...
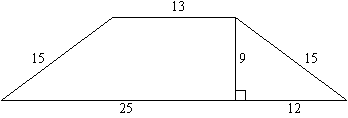Найдите площадь трапеции, изображённой на рисунке.
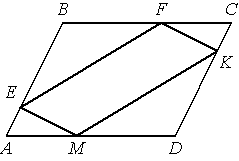В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём BF = DM, BE = DK. Докажите, что EFKM — параллелограмм.
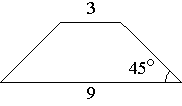В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BMC.
В треугольнике ABC DE – средняя линия. Площадь треугольника CDE равна 35. Найдите площадь треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: