
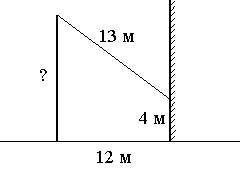
 От столба к дому натянут провод длиной 13 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
От столба к дому натянут провод длиной 13 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 12 м.
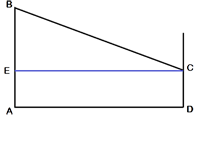 Изобразим рисунок схематично. Проведем отрезок СЕ, параллельный AD. AECD -
прямоугольник, т.к. все углы прямые. Следовательно, СЕ=AD и EA=CD.
Изобразим рисунок схематично. Проведем отрезок СЕ, параллельный AD. AECD -
прямоугольник, т.к. все углы прямые. Следовательно, СЕ=AD и EA=CD.
По
теореме Пифагора BC2=CE2+EB2
132=122+EB2
EB2=169-144
EB2=25
EB=5.
Высота столба = EB+EA=5+4=9.
Ответ: Высота столба - 9 метров.
Поделитесь решением
Присоединяйтесь к нам...
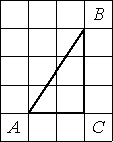 Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
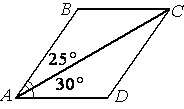 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.
Стороны AC, AB, BC треугольника ABC равны 2√
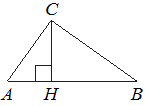 На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=4, BH=64. Найдите CH.
На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=4, BH=64. Найдите CH.
 В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.
Комментарии: