В треугольнике ABC угол C равен 90°, sinB=5/8, AB=16. Найдите AC.
sinB=AC/AB (по определению синуса).
sinB=AC/AB=5/8
AC/16=5/8
AC=16*5/8=2*5=10
Ответ: 10
Поделитесь решением
Присоединяйтесь к нам...
Сторона равностороннего треугольника равна 14√3. Найдите медиану этого треугольника.
Какой угол (в градусах) описывает часовая стрелка за 2 часа 2 минуты?
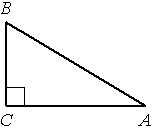В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB.
Боковые стороны AB и CD трапеции ABCD равны соответственно 18 и 30, а основание BC равно 3. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Проектор полностью освещает экран A высотой 50 см, расположенный на расстоянии 140 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 260 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: