Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AC=36, MN=27. Площадь треугольника ABC равна 96. Найдите площадь треугольника MBN.
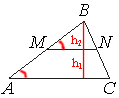Рассмотрим треугольники ABC и MBN.
∠ABC - общий.
∠BAC=∠BMN
Следовательно, по первому признаку подобия, эти треугольники подобны.
Площади треугольника ABC:
SABC=(1/2)AC*h1
96=(1/2)*36*h1
h1=96*2/36=96/18=32/6
Из подобия треугольников получаем пропорцию:
AC/MN=h1/h2
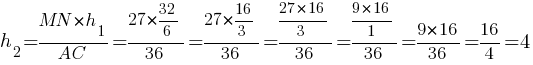
Тогда площадь треугольника MBN:
SMBN=(1/2)MN*h2
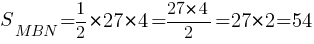
Ответ: 54
Поделитесь решением
Присоединяйтесь к нам...
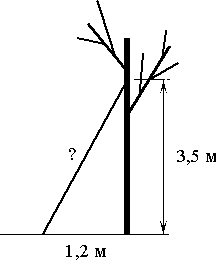Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 3,5 м над землёй, а нижний отстоит от ствола дерева на 1,2 м?
Основание AC равнобедренного треугольника ABC равно 8. Окружность радиуса 5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Касательные к окружности с центром O в точках A и B пересекаются под углом 82°. Найдите угол ABO. Ответ дайте в градусах.
В параллелограмме KLMN точка A — середина стороны LM. Известно, что KA=NA. Докажите, что данный параллелограмм — прямоугольник.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 135°, а CD=36.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: