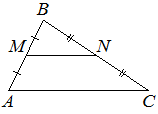
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 48, сторона BC равна 57, сторона AC равна 72. Найдите MN.
MN -
средняя треугольника по определению.
Тогда, по теореме о средней линии:
MN=AC/2=72/2=36
Ответ: 36
Поделитесь решением
Присоединяйтесь к нам...
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=2, а расстояние от точки K до стороны AB равно 1.
На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=32, MD=8, H — точка пересечения высот треугольника ABC. Найдите AH.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 169°, угол ABC равен 160°. Найдите угол ACB. Ответ дайте в градусах.
В треугольнике ABC DE – средняя линия. Площадь треугольника CDE равна 35. Найдите площадь треугольника ABC.
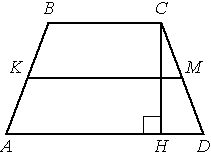В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 6.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: