
 Один из углов ромба равен 114°. Найдите меньший угол этого ромба. Ответ дайте в градусах.
Один из углов ромба равен 114°. Найдите меньший угол этого ромба. Ответ дайте в градусах.
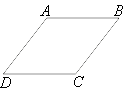 По свойству ромба:
По свойству ромба:
∠A=∠C - больший угол.
∠B=∠D - меньший угол.
Так как AB||CD (по определению ромба), то AD можно рассматривать как секущую.
Тогда ∠A+∠D=180° (так как это
односторонние углы).
∠D=180°-∠A=180°-114°=66°
Ответ: 66
Поделитесь решением
Присоединяйтесь к нам...
 Центральный угол AOB опирается на хорду АВ длиной 6. При этом угол ОАВ равен 60°. Найдите радиус окружности.
Центральный угол AOB опирается на хорду АВ длиной 6. При этом угол ОАВ равен 60°. Найдите радиус окружности.
 В треугольнике со сторонами 2 и 4 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 2. Чему равна высота, проведённая ко второй стороне?
В треугольнике со сторонами 2 и 4 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 2. Чему равна высота, проведённая ко второй стороне?
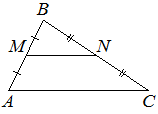 Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 48, сторона BC равна 57, сторона AC равна 72. Найдите MN.
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 48, сторона BC равна 57, сторона AC равна 72. Найдите MN.
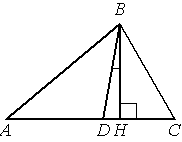 В треугольнике АВС углы А и С равны 40° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
В треугольнике АВС углы А и С равны 40° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
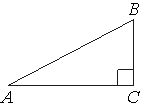 В треугольнике ABC угол C равен 90°, AC=4, AB=5. Найдите sinB.
В треугольнике ABC угол C равен 90°, AC=4, AB=5. Найдите sinB.
Комментарии: