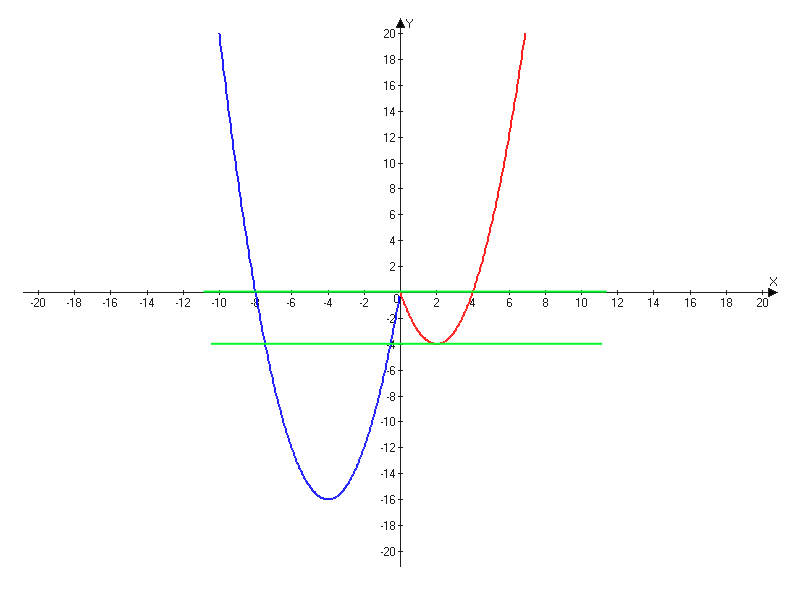
Постройте график функции y=x2-6|x|+2x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
В данной функции присутствуем
модуль, следовательно функцию надо разложить на две подфункции, в зависимости от значения
модуля:
x2-6x+2x, при x≥0
x2-6(-x)+2x, при x<0
x2-4x, при x≥0
x2+8x, при x<0
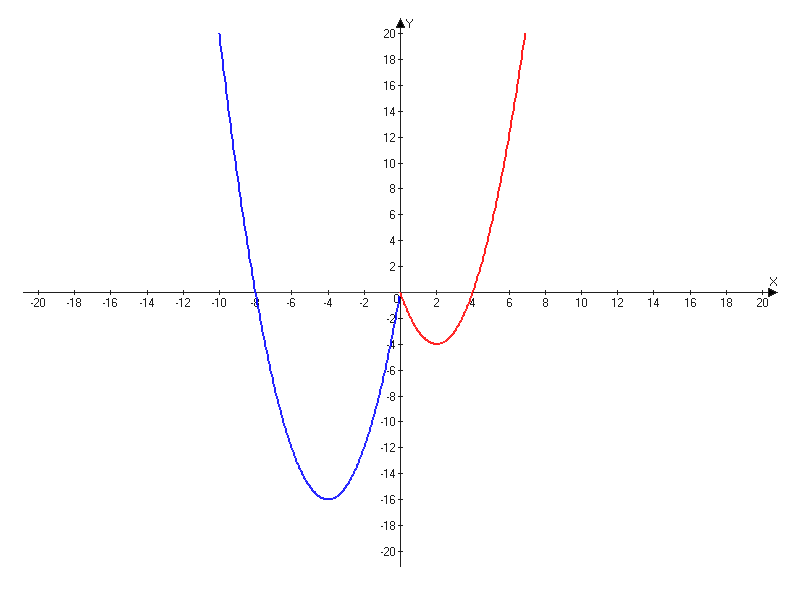
Рассмотрим и построим график для каждой подфункции и объединим их.
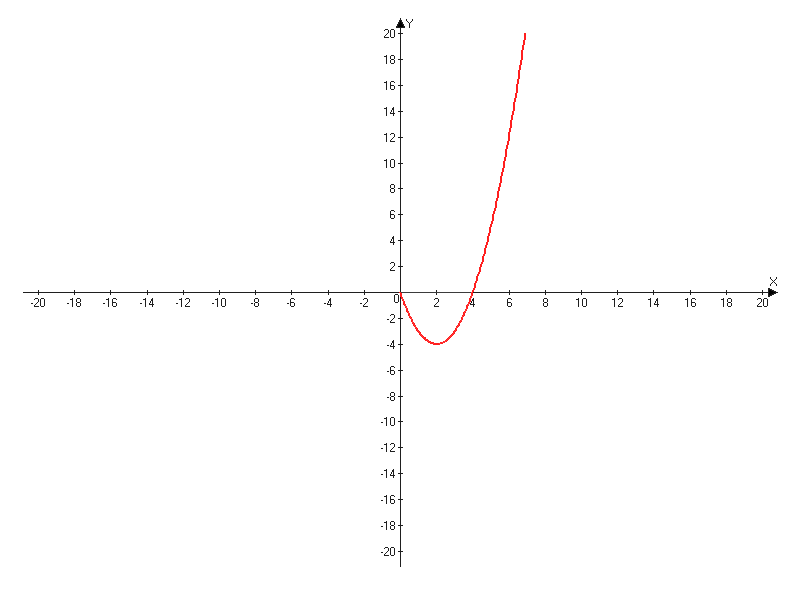
1) y1=x2-4x, при x≥0
| X | 0 | 1 | 2 | 4 |
| Y | 0 | -3 | -4 | 0 |
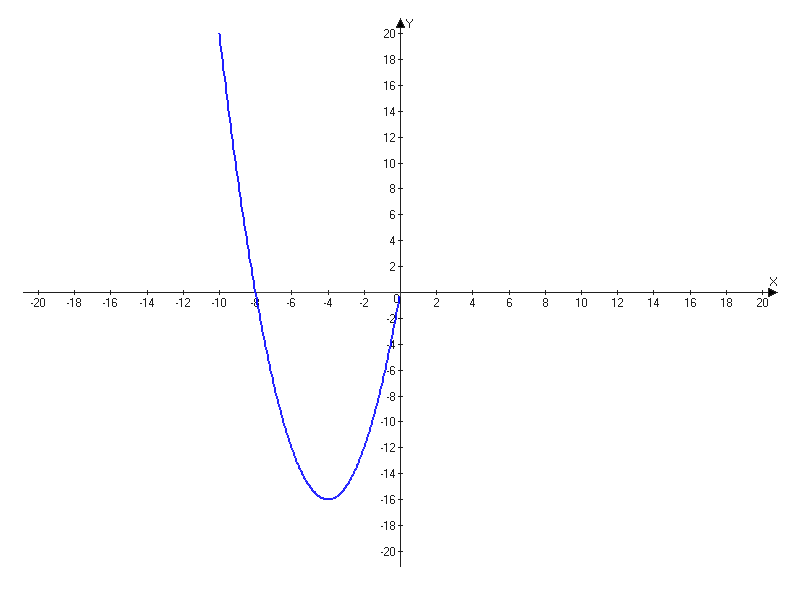
| X | 0 | -1 | -2 | -3 |
| Y | 0 | -7 | -12 | -15 |
Поделитесь решением
Присоединяйтесь к нам...
Две прямые пересекаются в точке C (см. рис.). Найдите абсциссу точки C.
Найдите все значения k, при каждом из которых прямая y=kx имеет с графиком функции y=-x2-0,25 ровно одну общую точку. Постройте этот график и все такие прямые.
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ
А) 
Б) 
В) 
КОЭФФИЦИЕНТЫ
1) k<0, b<0
2) k>0, b>0
3) k>0, b<0
В таблице под каждой буквой укажите соответствующий номер.
Постройте график функции
-x2, если |x|≤1
1/x, если |x|>1
и определите, при каких значениях c прямая y=c будет иметь с графиком единственную общую точку.
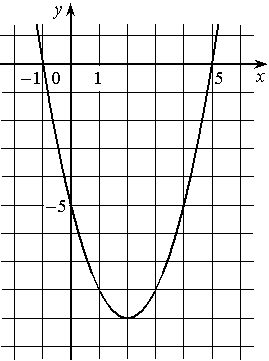На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) f(x)<0 при -1<x<5
2) Функция возрастает на промежутке [2; +∞)
3) Наименьшее значение функции равно -5
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-02-26 17:16:39) Администратор: Лида, посмотрите задачу №121, очень похожа на Вашу.
(2017-02-26 14:34:41) Лида: Постройте график функции y=x²-|8x+1| и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.
(2015-05-21 20:38:16) Администратор: Фая, почему область? Только при с=0 и с=-4 будет ровно три общие точки, а в области (-4;0) будет 4 точки.
(2015-05-20 16:01:12) Фая: ответ с принадлежит область от 0 до -4!