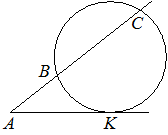
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=4, BC=32. Найдите AK.
По
теореме о касательной и секущей:
AK2=AB*AC
AK2=4*32=128
AK=√128=√4*32=√4*4*8=√4*4*4*2=
По первому свойству арифметического корня:
=√4*√4*√4*√2=2*2*2*√2=8√2
Ответ: 8√2
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) Если один из углов треугольника прямой, то треугольник прямоугольный.
2) Диагонали квадрата точкой пересечения делятся пополам.
3) Точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к этому отрезку.
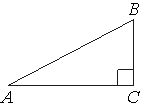В треугольнике ABC угол C равен 90°, AC=4, AB=5. Найдите sinB.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24, BF=32.
Какие из данных утверждений верны? Запишите их номера.
1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
2) Площадь круга меньше квадрата длины его диаметра.
3) Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник — ромб.
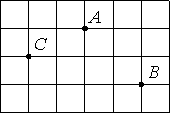На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
Хочу получать новые решения
Ни какого спама
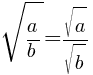, если a≥0, b≥0.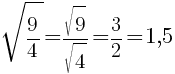
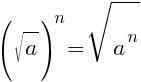, при a≥0.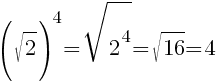
Автор: Таська
Комментарии: