
Косинус острого угла A треугольника ABC равен 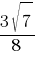 . Найдите sinA.
. Найдите sinA.
Применим основную тригонометрическую формулу:
sin2A+cos2A=1
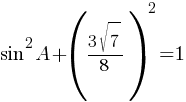

По второму правилу действий со степенями:
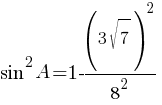
По первому правилу действий со степенями:

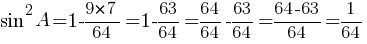
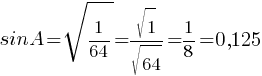 (использовали второе свойство арифметического корня)
(использовали второе свойство арифметического корня)
Ответ: 0,125
Поделитесь решением
Присоединяйтесь к нам...
 В трапеции ABCD AB=CD, ∠BDA=62° и ∠BDC=42°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, ∠BDA=62° и ∠BDC=42°. Найдите угол ABD. Ответ дайте в градусах.
 Площадь прямоугольного треугольника равна 968√
Площадь прямоугольного треугольника равна 968√
 В трапеции ABCD AB=CD, ∠BDA=35° и ∠BDC=58°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, ∠BDA=35° и ∠BDC=58°. Найдите угол ABD. Ответ дайте в градусах.
 Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=12, а расстояние от точки K до стороны AB равно 9.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=12, а расстояние от точки K до стороны AB равно 9.
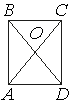 Диагонали AC и BD прямоугольника ABCD пересекаются
в точке O, BO=37, AB=56. Найдите AC.
Диагонали AC и BD прямоугольника ABCD пересекаются
в точке O, BO=37, AB=56. Найдите AC.
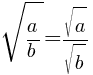 , если a≥0, b≥0.
, если a≥0, b≥0.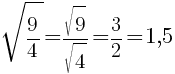
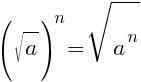 , при a≥0.
, при a≥0.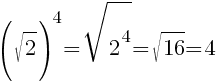
Комментарии: