Косинус острого угла A треугольника ABC равен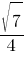 
. Найдите sinA.
Применим основную тригонометрическую формулу:
sin2A+cos2A=1
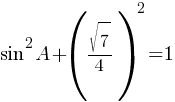
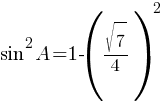
По правилам действий со степенями:
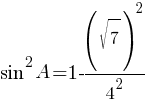
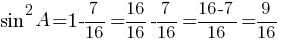
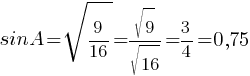
Ответ: 0,75
Поделитесь решением
Присоединяйтесь к нам...
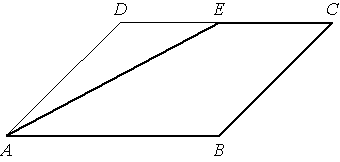Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB.
На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=15, MD=3, H — точка пересечения высот треугольника ABC. Найдите AH.
Точка О – центр окружности, /BOC=110° (см. рисунок). Найдите величину угла BAC (в градусах).
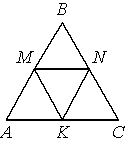В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что АMNK — ромб.
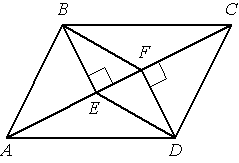В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DЕ параллельны.
Хочу получать новые решения
Ни какого спама
Автор: Таська
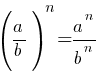
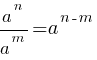
Комментарии: