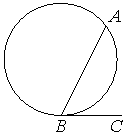На окружности отмечены точки A и B так, что меньшая дуга AB равна 152°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Проведем радиусы к точкам A и B, как показано на рисунке.
∠AOB - центральный и опирается на дугу в 152°, следовательно:
∠AOB=152°
Треугольник AOB - равнобедренный, так как две его стороны - это радиусы окружности.
Тогда, по свойству равнобедренного треугольника, углы при основании равны, обозначим их α.
По
теореме о сумме углов треугольника:
∠AOB+∠OAB+∠OBA=180°
152°+α+α=180°
2α=180°-152°=28°
α=28°/2=14°
По
свойству касательной ∠OBC=90°.
∠ABC=∠OBC-∠OBA
∠ABC=90°-14°=76°
Ответ: 76
Поделитесь решением
Присоединяйтесь к нам...
Найдите площадь треугольника, изображённого на рисунке.
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76. Найдите углы ромба.
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
В трапеции ABCD AB=CD, ∠BDA=49° и ∠BDC=13°. Найдите угол ABD. Ответ дайте в градусах.
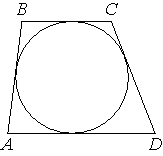Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=13, CD=22. Найдите AD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: