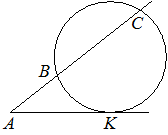
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=6, AC=54. Найдите AK.
По
теореме о касательной и секущей:
AK2=AB*AC
AK2=6*54=324
AK=√324=18
Ответ: 18
Поделитесь решением
Присоединяйтесь к нам...
Окружности радиусов 3 и 33 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
В треугольнике со сторонами 15 и 3 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?
Найдите площадь треугольника, изображённого на рисунке.
Площадь равнобедренного треугольника равна 144√
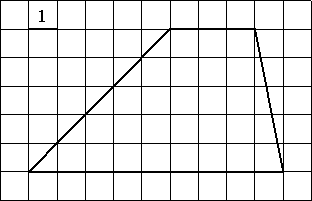Найдите площадь трапеции, изображённой на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: