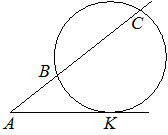
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности
в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=4, AC=64. Найдите AK.
По
теореме о касательно и секущей:
AK2=AB*AC
AK2=4*64
AK2=256
AK=√
Ответ: 16
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 155°. Найдите угол C. Ответ дайте в градусах.
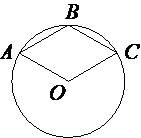Точка O – центр окружности, на которой лежат точки A, B и C таким образом, что OABC – ромб. Найдите угол ABC. Ответ дайте в градусах.
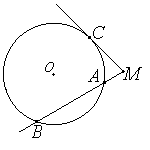
На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=27, MD=18, H — точка пересечения высот треугольника ABC. Найдите AH.
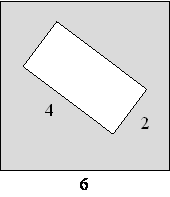Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2022-04-01 03:27:21) мария: Радиус окружности, вписанной в трапецию, равен 18. Найдите высоту этой трапеции
(2021-04-01 23:34:01) марк: в треугольнике авс угол с равен 90 градусо
(2021-02-13 17:11:07) ааа: Тут + вместо умножения должен быть