
 На стороне AB треугольника ABC взята точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=12, BC=18 и CD=8.
На стороне AB треугольника ABC взята точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=12, BC=18 и CD=8.
Прямая и окружность могут располагаться относительно друг друга в трех вариантах:
1) Не пересекаться, то есть не иметь ни одной общей точки.
2) Касаться, то есть иметь только одну общую точку, тогда прямая называется
касательной к окружности.
3) Пересекаться, то есть иметь две общие точки.
В условии задачи сказано, что окружность проходит через точку С и касается прямой ВС. Значит прямая ВС кроме точки касания других общих точек с окружностью иметь не может, следовательно, окружность касается с прямой ВС в точке С (как показано на рисунке).
Рассмотрим треугольники ABC и CDB.
∠B - общий
∠DAC является
вписанным в окружность и опирается на дугу CD. Т.е. равен половине ее градусной меры.
∠BCD обхватывает дугу CD как
касательная и
хорда и тоже равен половине градусной меры дуги CD (по
четвертому свойству углов).
Следовательно, углы DAC и BCD равны.
Тогда, по
первому признаку подобия треугольников, эти треугольники
подобны.
Следовательно:
AC/CD=BC/BD=AB/BC
AC/CD=BC/BD
12/8=18/BD =>BD=8*18/12=2*18/3=2*6=12
BC/BD=AB/BC
18/12=AB/18 => AB=18*18/12=9*18/6=9*3=27
AD=AB-BD=27-12=15
Ответ: 15
Поделитесь решением
Присоединяйтесь к нам...
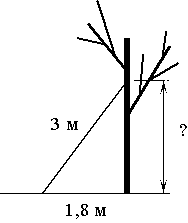 Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
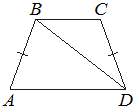 В трапеции ABCD известно, что AB=CD, ∠BDA=38° и ∠BDC=32°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD известно, что AB=CD, ∠BDA=38° и ∠BDC=32°. Найдите угол ABD. Ответ дайте в градусах.
 Сторона квадрата равна 38√2. Найдите радиус окружности, описанной около этого квадрата.
Сторона квадрата равна 38√2. Найдите радиус окружности, описанной около этого квадрата.
 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
 Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
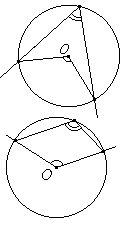 Вписанный угол либо равен половине соответствующего ему центрального угла, либо дополняет половину этого угла до 180°.
Вписанный угол либо равен половине соответствующего ему центрального угла, либо дополняет половину этого угла до 180°.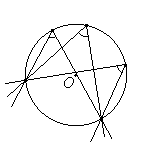 Углы, вписанные в одну окружность и опирающиеся на одну и ту же дугу, равны.
Углы, вписанные в одну окружность и опирающиеся на одну и ту же дугу, равны.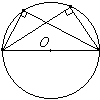 Вписанный угол, опирающийся на диаметр, равен 90°.
Вписанный угол, опирающийся на диаметр, равен 90°.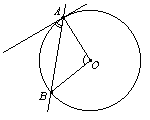 Угол, образованный касательной к окружности и секущей, проведенной через точку касания, равен половине дуги, заключенной между его сторонами.
Угол, образованный касательной к окружности и секущей, проведенной через точку касания, равен половине дуги, заключенной между его сторонами.
Комментарии: