В прямоугольнике одна сторона равна 96, а диагональ равна 100. Найдите площадь прямоугольника.
Площадь
прямоугольника равна произведению его сторон.
По
определению, все углы прямоугольника прямые, следовательно, диагональ и две стороны образуют
прямоугольный треугольник.
Следовательно, мы можем применить
теорему Пифагора, обозначим длину неизвестной стороны как "х":
962+x2=1002
x2=1002-962
Можно вычислить "в лоб", а можно немного облегчить себе задачу, применив формулу
разность квадратов:
x2=(100-96)(100+96)
x2=4*196
x=√
S=96*28=2688
Ответ: 2688
Поделитесь решением
Присоединяйтесь к нам...
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 2. Найдите площадь трапеции.
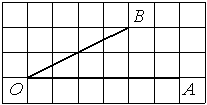Найдите тангенс угла AOB, изображённого
на рисунке.
Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Основания трапеции относятся как 2:3. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции?
Медиана равностороннего треугольника равна 13√3. Найдите его сторону.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: