Укажите неравенство, решение которого изображено на рисунке.
1) x2-49≤0
2) x2+49≤0
3) x2-49≥0
4) x2+49≥0
Посмотрим на предложенные неравенства:
- все они квадратичные, т.е. графики этих функций - параболы
- у всех аргумент "а" равен единице, т.е. больше нуля, следовательно ветви их парабол направлены вверх
- графики парабол 1) и 3) будут совпадать, т.к. это одинаковые функции.
- графики парабол 2) и 4) будут совпадать, т.к. это одинаковые функции.
Посмотрим на рисунок решения неравенства:
- корни квадратичной функции должны быть -7 и 7.
Решим уравнение x2-49=0
x2-72=0
Применим формулу разность квадратов:
(x-7)(x+7)=0
x-7=0 => x1=7
x+7=0 => x2=-7
Неравенства 1) и 3), судя по корням, подходят.
Решим уравнение x2+49=0
x2=-49
Данное уравнение не имеет корней, т.к. ни какое число, возведенное в квадрат не даст отрицательный результат. Значит неравенства 2) и 4) не подходят.
Посмотрим на рисунок, в условии показан диапазон, когда график функции ниже оси Х, т.е. меньше нуля, следовательно, подходит неравенство x2-49≤0
Ответ: 1)
Поделитесь решением
Присоединяйтесь к нам...
Решите неравенство (2x-5)2≥(5x-2)2.
Решите систему уравнений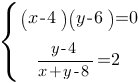 
.
Расстояние между пристанями А и В равно 48 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошёл 25 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 5 км/ч.
Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 20 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 210 км, скорость первого велосипедиста равна 20 км/ч, скорость второго — 30 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
Найдите корни уравнения 5x2+20x=0.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2024-01-30 19:45:49) Анжелика: Соотнести величины с формулой