
Укажите неравенство, решение которого изображено на рисунке.

1) x2-49>0
2) x2-49<0
3) x2+49<0
4) x2+49>0
Посмотрим на предложенные неравенства:
- все они квадратичные, т.е. графики этих функций - параболы
- у всех аргумент "а" равен единице, т.е. больше нуля, следовательно ветви их парабол направлены вверх
- графики парабол 1) и 2) будут совпадать, т.к. это одинаковые функции.
- графики парабол 3) и 4) будут совпадать, т.к. это одинаковые функции.
Посмотрим на рисунок решения неравенства:
- корни квадратичной функции должны быть -7 и 7.
 Решим уравнение x2-49=0
Решим уравнение x2-49=0
x2-72=0
Применим формулу разность квадратов:
(x-7)(x+7)=0
x-7=0 => x1=7
x+7=0 => x2=-7
Неравенства 1) и 2), судя по корням, подходят.
Решим уравнение x2+49=0
x2=-49
Данное уравнение не имеет корней, т.к. ни какое число, возведенное в квадрат не даст отрицательный результат. Значит неравенства 3) и 4) не подходят.
Посмотрим на рисунок, в условии показан диапазон, когда график функции выше оси Х, т.е. больше нуля, следовательно, подходит неравенство x2-49>0
Ответ: 1)
Поделитесь решением
Присоединяйтесь к нам...
Городской бюджет составляет 27 млн рублей, а расходы на одну из его статей составили 10%. Сколько рублей потрачено на эту статью бюджета?
Решите уравнение 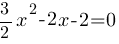 .
.
Решите уравнение x6=(6x-5)3.
На каком рисунке изображено множество решений неравенства
3-4x>11-8(x-2)?
1) 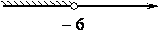
2) 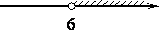
3) 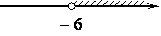
4) 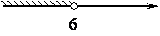
Расстояние от Солнца до Земли свет проходит примерно за 8,3 минуты. Найдите приблизительно расстояние от Солнца до Земли, ответ округлите до миллионов км. Скорость света равна 300000 км/с.
Комментарии: