Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 250 см от проектора. На каком наименьшем расстоянии
(в сантиметрах) от проектора нужно расположить экран B высотой 160 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
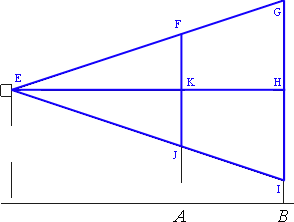Обозначим треугольники и их ключевые точки как показано на рисунке.
Рассмотрим треугольники EGI и EFJ.
Прямая EH перпендикулярна обоим экранам и проходит через их центр, следовательно является
серединным перпендикуляром.
То есть, FK=FJ/2=80/2=40 и GH=GI/2=160/2=80.
Рассмотрим треугольники EFK и EGH.
∠FEK - общий для обоих треугольников.
∠EKF=∠EHG=90° (т.к. EH -
серединный перпендикуляр).
Тогда, по
первому признаку подобия, данные треугольники
подобны.
Следовательно, мы можем записать пропорцию сторон:
EH/EK=GH/FK
EH/250=80/40
EH=(250*80)/40=250*2=500
Ответ: 500
Поделитесь решением
Присоединяйтесь к нам...
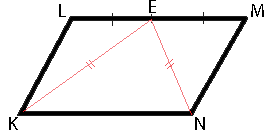В параллелограмме KLMN точка E — середина стороны LM. Известно, что EK=EN. Докажите, что данный параллелограмм — прямоугольник.
В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=86, SQ=43.
Сторона ромба равна 40, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Докажите, что медиана треугольника делит его на два треугольника, площади которых равны между собой.
Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=13.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: