Дана арифметическая прогрессия (an), разность которой равна 0,6, a1=6,2. Найдите сумму первых 13 её членов.
Чтобы найти сумму
арифметической прогрессии у нас есть
формулы.
Воспользуемся второй формулой.
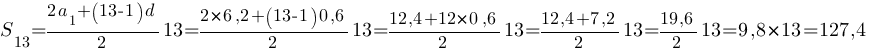
Ответ: S13=127,4
Поделитесь решением
Присоединяйтесь к нам...
В первом ряду кинозала 50 мест, а в каждом следующем на 1 больше, чем в предыдущем. Сколько мест в седьмом ряду?
Выписаны первые три члена арифметической прогрессии:
-6; 1; 8; ...
Найдите 6-й член этой прогрессии.
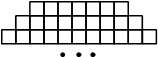Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 2 квадрата больше, чем в предыдущей. Сколько квадратов в 39-й строке?
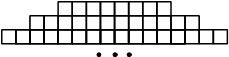Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 4 квадрата больше, чем в предыдущей. Сколько квадратов в 54-й строке?
В первом ряду кинозала 25 мест, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в шестом ряду?
Хочу получать новые решения
Ни какого спама
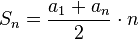, где a1 - первый член прогрессии, an - член с номером n, n — количество суммируемых членов.
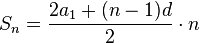, где a1 — первый член прогрессии, d — разность прогрессии, n — количество суммируемых членов. 
Автор: Таська
Комментарии: