
 Длина хорды окружности равна 130, а расстояние от центра окружности до этой хорды равно 72. Найдите диаметр окружности.
Длина хорды окружности равна 130, а расстояние от центра окружности до этой хорды равно 72. Найдите диаметр окружности.
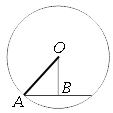 Обозначим ключевые точки, как показано на рисунке. Проведем отрезок АО.
Обозначим ключевые точки, как показано на рисунке. Проведем отрезок АО.
Рассмотрим треугольник AOB.
Данный треугольник
прямоугольный, так как расстояние ОВ является
высотой (кротчайшее расстояние).
AB равна половине длины
хорды (по
третьему свойству хорды).
Тогда, по
теореме Пифагора:
AO2=OB2+AB2
AO2=722+(130/2)2
AO2=5184+4225=9409
AO=97 - это радиус окружности, следовательно, диаметр:
D=2*AO=2*97=194
Ответ: 194
Поделитесь решением
Присоединяйтесь к нам...
 Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 4. Найдите радиус окружности.
Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 4. Найдите радиус окружности.
 На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 5 м?
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 5 м?
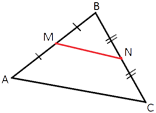 Точки M и N являются серединами сторон AB и BC треугольника ABC, AC=24. Найдите MN.
Точки M и N являются серединами сторон AB и BC треугольника ABC, AC=24. Найдите MN.
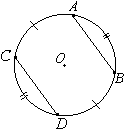
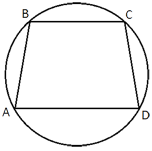 Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.
Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.
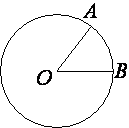 На окружности с центром O отмечены точки A и B так, что
/AOB=66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги.
На окружности с центром O отмечены точки A и B так, что
/AOB=66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги.

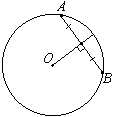
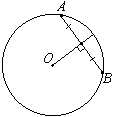
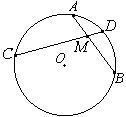
Комментарии:
(2024-05-16 18:52:08) Милана: Дана окружность с центром О, через который проходят две хорды. Найди < D AB, если