
 В трапеции ABCD основания AD и BC равны соответственно 48 и 3, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=3.
В трапеции ABCD основания AD и BC равны соответственно 48 и 3, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=3.
Продлим стороны AB и CD до пересечения друг с другом.
 Рассмотрим треугольник AED.
Рассмотрим треугольник AED.
По
теореме о сумме углов треугольника:
180°=∠EDA+∠DAE+∠AED
180°=90°+∠AED
∠AED=90°
Следовательно треугольник AED -
прямоугольный.
Рассмотрим треугольники AED и BEC.
∠AED - общий
∠EBC=∠EAD (т.к. это
соответственные углы)
Треугольники AED и BEC
подобны (по
первому признаку подобия треугольников).
Тогда по
определению подобия:
AD/BC=AE/BE
AD/BC=(AB+BE)/BE
48/3=(3+BE)/BE
16BE=3+BE
15BE=3
BE=1/5=0,2
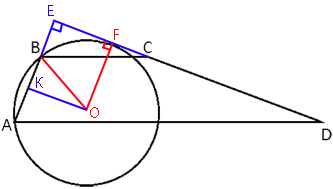 Точка F - точка касания прямой CD и окружности.
Точка F - точка касания прямой CD и окружности.
По
теореме о касательной и секущей:
EF2=BE*AE=BE*(AB+BE)=0,2(3+0,2)=0,64
EF=0,8
Рассмотрим треугольник BOK.
О - центр окружности
OB - радиус окружности
OK -
серединный перпендикуляр к
хорде AB (
третье свойство хорды)
OK=EF (т.к. KEFO -
прямоугольник)
KB=AB/2 (т.к. OK -
серединный перпендикуляр)
По
теореме Пифагора:
OB2=OK2+KB2
OB2=0,82+(3/2)2
OB2=0,64+2,25=2,89
OB=1,7
Ответ: R=1,7
Поделитесь решением
Присоединяйтесь к нам...
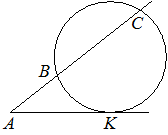 Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=6, AC=54. Найдите AK.
Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=6, AC=54. Найдите AK.
 В треугольнике ABC угол C равен 90°, BC=6, sinA=0,6. Найдите AB.
В треугольнике ABC угол C равен 90°, BC=6, sinA=0,6. Найдите AB.
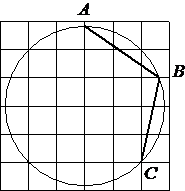 Найдите угол ABC . Ответ дайте в градусах.
Найдите угол ABC . Ответ дайте в градусах.
 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
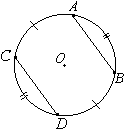
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKD.

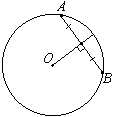
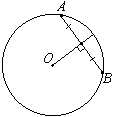
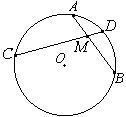
Комментарии:
(2020-12-28 11:15:48) алина????: в равнобедренную трапецию периметр которой равен 200, а площадь 2000, можно вписать окружность. найдите расстояние от точки пересечения диагоналей трапеции до ее меньшего основания.
(2016-12-18 17:24:48) Администратор: Нора, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2016-12-17 12:33:30) Нора: Отрезок АВ разделен точками С и Д так что, АС:ВС-7:8, АД:ВД=13:17,Найти длину отрезка АВ, если СД=2см
(2016-10-20 18:50:10) Администратор: Дмитрий, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2016-10-20 16:49:36) Дмитрий: ABCD-равнобедренная трапеция,AB=2,OK=1,Найти:BC,EF-?
(2016-10-14 22:46:17) Магомед: Ребята, не задавайте лишних вопросов. Все правильно решено.
(2015-05-31 22:49:47) Юлия: Все, нашла свою ошибку :)) С условием все в порядке!
(2015-05-29 14:51:59) Юлия: Послушайте, народ! Может быть я чего-то не понимаю, но мне кажется, что задача некорректна. Дело вот в чем. Я провела две высоты ВН и СК. Получается,что углы АВН и СДК равны. Тогда треугольники АВН и СДК равны по катету и острому углу.Причем АН=СК и ВН=КД, но высоты ВН и СК равны, поэтому ВН=АН=СК=КД. Тогда трапеция равнобедренная, причем АН=(48-3)/2=22,5. Но тогда в треугольнике АВН катет больше гипотенузы!!! Я где-то наврала??? Просто сыну такая же задача попалась в среду на ОГЭ, мне интересно...
(2015-05-17 23:40:22) Администратор: По третьему свойству хорды, посмотрите ссылку в решении.
(2015-05-17 10:58:39) : Почему ОК срединный перпендикуляр
(2015-05-17 10:58:35) : Почему ОК срединный перпендикуляр
(2014-05-26 22:08:21) Администратор: Альбина, сказано, что окружность касается ПРЯМОЙ CD, а не стороны CD и не отрезка CD. Значит окружность может касаться продолжения отрезка CD.
(2014-05-26 19:51:27) Альбина: В условии сказано, что окружность касается CD, а у вас она касается продолжения CD/
(2014-05-25 18:39:45) Администратор: Татьяна, перейдите по ссылке по свойствам хорды. Там есть вся информация.
(2014-05-25 16:50:53) Татьяна: О чем речь в третьем свойстве хорды? напомните, пожалуйста
(2014-05-22 15:42:21) Вероника: Большое спасибо !!!Отличный сайт, все очень понятно объяснили,!
(2014-05-20 22:08:49) Администратор: OF=OB, так как это радиусы окружности.
(2014-05-20 21:45:40) : а почему OF=OB?
(2014-05-20 21:41:23) : очепятка))ахаха))
(2014-05-20 21:33:16) : очепятка))ахаха))