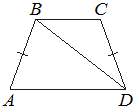
В трапеции ABCD известно, что AB=CD, ∠BDA=38° и ∠BDC=32°. Найдите угол ABD. Ответ дайте в градусах.
Трапеция ABCD
равнобедренная, так как AB=CD.
Следовательно, по второму свойству равнобедренной трапеции:
∠BAD=∠CDA=∠BDA+∠BDC=38°+32°=70°
Рассмотрим треугольник ABD.
По
теореме о сумме углов треугольника:
180°=∠BAD+∠BDA+∠ABD
180°=70°+38°+∠ABD
∠ABD=180°-70°-38°=72°
Ответ: 72
Поделитесь решением
Присоединяйтесь к нам...
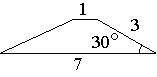Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 1 и 7.
Сторона квадрата равна 3√2. Найдите диагональ этого квадрата.
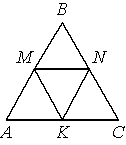В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равносторонний.
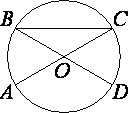В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 130°. Найдите вписанный угол ACB. Ответ дайте в градусах.
В окружности с центром в точке O проведены диаметры AD и BC, угол OAB равен 70°. Найдите величину угла OCD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: