В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 13 и 7. Найдите площадь параллелограмма ABCD.
По
свойству касательной:
OF - радиус окружности, т.к. OF проходит через центр окружности и перпендикулярен
касательной AC.
AG=AF
BG=BH=x
CH=CF=y
AF найдем по
теореме Пифагора:
AO2=AF2+OF2
252=AF2+72
625=AF2+49
AF2=576
AF=24=AG
EH -
высота параллелограмма. EH=OH+OE=7+13=20
SABC=p*r, где p - полупериметр, r - радиус вписанной окружности.
p=(AB+BC+AC)/2.
Рассмотрим треугольники ABC и CDA.
AD=BC и AB=CD (по
свойству параллелограмма).
AC - общая сторона.
Следовательно, по
третьему признаку равенства треугольников, данные треугольники равны.
Тогда:
SABCD=2*SABC
И в тоже время SABCD=EH*AD.
Приравняем полученные равенства:
p*r=EH*AD/2
(AB+BC+AC)/2*r=EH*BC/2
(AG+GB+BH+HC+CF+AF)*r=EH*(BH+HC)
(24+x+x+y+y+24)*7=20*(x+y)
(48+2x+2y)*7=20*(x+y)
336+7(2x+2y)=20*(x+y)
336+14(x+y)=20*(x+y)
336=6(x+y)
x+y=56=BC=AD
SABCD=EH*AD=20*56=1120
Ответ: SABCD=1120
Поделитесь решением
Присоединяйтесь к нам...
На стороне AB треугольника ABC взята точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=12, BC=18 и CD=8.
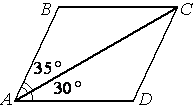Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите больший угол параллелограмма.
естница соединяет точки A и B и состоит из 40 ступеней. Высота каждой ступени равна 19,5 см, а длина – 40 см. Найдите расстояние между точками A и B (в метрах).
Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 45 и 46, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: