
 Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 60, тангенс угла BAC равен 5/12. Найдите радиус окружности, вписанной в треугольник ABC.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 60, тангенс угла BAC равен 5/12. Найдите радиус окружности, вписанной в треугольник ABC.
Вариант №1
Рассмотрим треугольники ABC и BCP.
∠ABC - общий.
∠ACB=∠BPC=90° (т.к. CP -
высота).
По
первому признаку подобия треугольников, данные треугольники
подобны.
Следовательно, BC/AC=BP/BC=BC/AB=k.
k - коэффициент подобия.
Заметим, что BC/AB - это sinA (по
определению), найдем его:
tgA=(sinA)/(cosA)=5/12
cosA=(12sinA)/5=2,4sinA
По основной тригонометрической формуле:
sin2A+cos2A=1
sin2A+(2,4sinA)2=1
sin2A+5,76sin2A=1
6,76sin2A=1
sin2A=1/6,76
sinA=1/2,6=k
Дальше тонкий момент:
По свойству подобных треугольников отношение периметров и длин биссектрис, медиан, высот и серединных перпендикуляров равно коэффициенту подобия.
Радиус
вписанной окружности имеет линейную зависимость от периметра треугольника (
третье свойство), следовательно отношение радиусов подобных треугольников тоже подчиняется коэффициенту подобия.
Т.е. r/R=k
R=r/k=60/(1/2,6)=60*2,6=156.
Ответ: R=156
Поделитесь решением
Присоединяйтесь к нам...
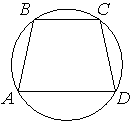 Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 52°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 52°. Найдите угол B этой трапеции. Ответ дайте в градусах.
 В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.
 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.
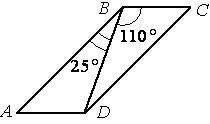 Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
25° и 110°. Найдите меньший угол параллелограмма.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
25° и 110°. Найдите меньший угол параллелограмма.
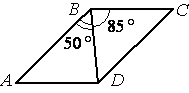 Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
50° и 85°. Найдите меньший угол параллелограмма.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
50° и 85°. Найдите меньший угол параллелограмма.
 .
.
Комментарии:
(2015-04-12 17:00:19) Администратор: AB2=144*CB2/25+CB2=144*CB2/25+25CB2/25=(144CB2+25CB2)/25=169CB2/25
(2015-04-12 16:52:31) : AB2=144*CB2/25+CB2 AB2=169*CB2/25 почему исчезло CB?
(2015-03-18 20:20:21) Администратор: Всеволод, напишите, мне пожалуйста, на zapros@otvet-gotov.ru, давайте дискутировать по почте, чтобы не "взрывать мозг" другим пользователям )
(2015-03-18 20:14:32) Администратор: Всеволод, большое Вам спасибо за такую упорную борьбу за истину. Дискутировать с таким оппонентом - одно удовольствие. В чем я с Вами согласен, так это в том, что использованная мной формула мало известна и, действительно, требует доказательства. Т.е. использовать ее как есть не очень корректно в данном случае. Но именно по этой же причине, некорректно утверждать, что R/r=k, это надо показать. Мы с Вами понимаем, что высоты, медианы и т.д. "подчиняются" коэффициенту подобия, площади подобных треугольников уже "не подчиняются". Для обычного школьника эти тонкости не очевидны. Вы меня убедили, что надо написать более корректное решение. Я этим займусь немного позже, сейчас очень много запросов на новые задачи. Еще раз спасибо Вам!
(2015-03-18 13:26:43) Всеволод: В учебнике А.В.Погорелова на стр. 154 есть определение подобия как преобразования, а потом несколько страниц достаточно подробно говорится о его свойствах и приводятся хорошие примеры. В учебнике под редакцией А.Н.Тихонова на стр. 138 о подобии сказано лишь: "В геометрии фигуры одинаковой формы принято называть подобными". Другие учебники не смотрел, но допускаю, что они могут существенно различаться. В Кодификаторе элементов ФИПИ есть пункт 7.1.6 "Преобразование плоскости. Движения. Симметрия." Да, сказано мало, но это про преобразование подобия. Мне кажется, что отношение соответствующих радиусов и высот у подобных треугольников доказывать не надо потому, что это является одним из основных свойств преобразования подобия. Согласен с тем, что на учебники, которые рассматривают сразу лишь признаки подобия треугольников без упоминания о преобразовании подобия так опереться не получится. Если считать, что определение подобия как преобразования в программе и учебниках отсутствует, то вы правы, нужно гонять известные формулы. Рассмотрим площадь треугольника S=(b*c*sinA)/2 (еще подойдёт формула Герона, но с проверкой всех учебников). Из неё выходит, что площади подобных треугольников относятся как квадрат их коэффициента подобия и об этом говорится везде. Тогда соответствующие радиусы и высоты тоже подобны с тем же коэффициентом, потому что везде есть формулы для площади S=a*b*c/4R, S=p*r и S=a*h/2. Вы использовали в решении формулу r=(a+b-c)/2, упоминание о которой не так просто будет найти в некоторых учебниках. Вообще, всегда можно попросить доказать все применённые в решении формулы и утверждения. Но тогда начинать придётся с "Начал" планиметрии или защищаться фразой "из программы", а это уже субстанция дискуссионная. Если же считать, что понятие преобразования подобия в программе всё же есть, то ссылка в решении на его свойства выглядит мощнее и легче, чем применение известных формул.
(2015-03-09 16:23:33) Администратор: Всеволод, Ваше решение в целом правильное, кроме одного НО. Вы ссылаетесь на свой "жизненный опыт", а не на теоремы или определения "Отношение радиусов вписанных окружностей у подобных треугольников тоже равно коэффициенту подобия". Это нужно доказать математически, а не голословно, даже, если это очевидно. "Ведь по определению подобия все линейные размеры фигуры увеличиваются в k раз (стороны, медианы, высоты, биссектрисы, диагонали и радиусы вписанной и описанной окружностей)" - в определении подобия ничего похожего нет. ОПР.: Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника. Все остальное надо доказывать в решении...Если я не прав, то пришлите, пожалуйста, ссылку на материалы, где подтверждаются Ваши слова.
(2015-03-07 16:55:58) Всеволод: Треугольники CBP и ABC подобны с коэффициентом подобия k=BC/AB, а это ведь sinA. Используя основное тригонометрическое тождество и определение tgA, можно найти sinA из системы: (sinA)^2+(cosA)^2=1 sinA/cosA=5/12=tgA Получается, что sinA=5/13 Отношение радиусов вписанных окружностей у подобных треугольников тоже равно коэффициенту подобия. Ведь по определению подобия все линейные размеры фигуры увеличиваются в k раз (стороны, медианы, высоты, биссектрисы, диагонали и радиусы вписанной и описанной окружностей). Итак, соотношение радиусов у нас равно r/R=5/13,откуда R=156.