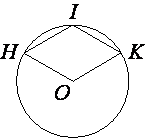Точка O – центр окружности, на которой лежат точки H, I и K таким образом, что OHIK – ромб. Найдите угол OHI. Ответ дайте в градусах.
HO=KO (т.к. это радиусы окружности)
HO=KO=HI=IK (по
определению ромба)
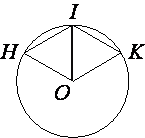Проведем отрезок OI.
OI тоже радиус окружности, следовательно HO=KO=HI=IK=OI
Следовательно, треугольники HIO и KIO -
равносторонние, а все углы равностороннего треугольника равны 60° (по
свойству).
Следовательно, /OHI=60°
Ответ: 60
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 57. Найдите площадь четырёхугольника ABMN.
В треугольнике ABC известно, что AB=6, BC=10, sin∠ABC=1/3. Найдите площадь треугольника ABC.
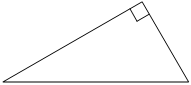В прямоугольном треугольнике катет и гипотенуза равны 16 и 34 соответственно. Найдите другой катет этого треугольника.
Укажите номера верных утверждений.
1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
2) Вертикальные углы равны.
3) Любая биссектриса равнобедренного треугольника является его медианой.
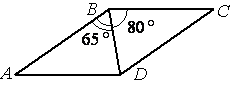Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 80°. Найдите меньший угол параллелограмма.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: