
 Один из углов ромба равен 114°. Найдите меньший угол этого ромба. Ответ дайте в градусах.
Один из углов ромба равен 114°. Найдите меньший угол этого ромба. Ответ дайте в градусах.
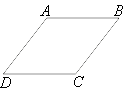 По свойству ромба:
По свойству ромба:
∠A=∠C - больший угол.
∠B=∠D - меньший угол.
Так как AB||CD (по определению ромба), то AD можно рассматривать как секущую.
Тогда ∠A+∠D=180° (так как это
односторонние углы).
∠D=180°-∠A=180°-114°=66°
Ответ: 66
Поделитесь решением
Присоединяйтесь к нам...
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
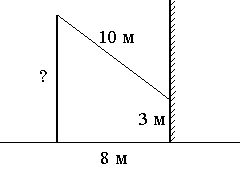 От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м.
От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м.
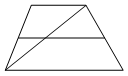 Основания трапеции равны 8 и 18. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Основания трапеции равны 8 и 18. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
 Площадь равнобедренного треугольника равна 144√
Площадь равнобедренного треугольника равна 144√
 В треугольнике ABC угол C равен 90°, BC=5, AC=2.
В треугольнике ABC угол C равен 90°, BC=5, AC=2.
Найдите tgB.
Комментарии: