Сторона ромба равна 8, а расстояние от точки пересечения диагоналей ромба до неё равно 2. Найдите площадь этого ромба.
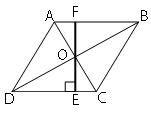Обозначим ключевые точки как показано на рисунке.
Проведем продолжение высоты OE к стороне AB и обозначим точку пересечения как F (как показано на рисунке).
Площадь
ромба (как и
параллелограмма) равна произведению высоты на сторону ромба.
Высота ромба = EF (т.к. EF перпендикулярна CD). Рассмотрим треугольники DOE и BOF.
DO=OB (по второму
свойству ромба)
∠DOE=∠BOE (т.к. они
вертикальные)
∠EDO=∠FBO (т.к. это
внутренние накрест-лежащие)
Следовательно, треугольники DOE и BOF равны по
второму признаку.
Тогда OE=OF => EF=2*OE=2*2=4
Sромба=EF*CD=4*8=32
Ответ: Sромба=32
Поделитесь решением
Присоединяйтесь к нам...
Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 44°, 71° и 65°.
В трапецию, сумма длин боковых сторон которой равна 18, вписана окружность. Найдите длину средней линии трапеции.
Человек, рост которого равен 1,8 м, стоит на расстоянии 4 м от уличного фонаря. При этом длина тени человека равна 1 м. Определите высоту фонаря (в метрах).
Высота BH ромба ABCD делит его сторону AD на отрезки AH=4 и HD=1. Найдите площадь ромба.
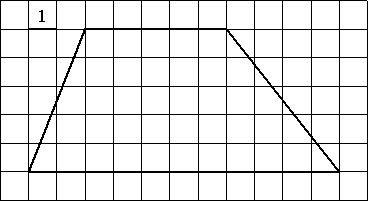Найдите площадь трапеции, изображённой на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2022-11-20 14:01:01) Артемий: докажите, что четырехугольник изображенный на клетчатой бумаге имеет два равных угла