
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ726 –Є–Ј 1087 |
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ BE –Є –Љ–µ–і–Є–∞–љ–∞ AD –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ—Л –Є –Є–Љ–µ—О—В –Њ–і–Є–љ–∞–Ї–Њ–≤—Г—О –і–ї–Є–љ—Г, —А–∞–≤–љ—Г—О 164. –Э–∞–є–і–Є—В–µ —Б—В–Њ—А–Њ–љ—Л —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ BE –Є –Љ–µ–і–Є–∞–љ–∞ AD –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ—Л –Є –Є–Љ–µ—О—В –Њ–і–Є–љ–∞–Ї–Њ–≤—Г—О –і–ї–Є–љ—Г, —А–∞–≤–љ—Г—О 164. –Э–∞–є–і–Є—В–µ —Б—В–Њ—А–Њ–љ—Л —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC.
–Т–∞—А–Є–∞–љ—В вДЦ1
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ABD.
BO –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–µ–љ AD (–њ–Њ —Г—Б–ї–Њ–≤–Є—О –Ј–∞–і–∞—З–Є), —В.–µ. ∠BOD=∠BOA=90¬∞.
∠ABO=∠DBO (—В.–Ї. BE -
–±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞).
–Я–Њ–ї—Г—З–∞–µ—В—Б—П, —З—В–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є ABO –Є DBO —А–∞–≤–љ—Л (–њ–Њ
–≤—В–Њ—А–Њ–Љ—Г –њ—А–Є–Ј–љ–∞–Ї—Г —А–∞–≤–µ–љ—Б—В–≤–∞ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤).
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, AB=BD.
–Ґ.–µ. —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ABD -
—А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ—Л–є.
BO -
–±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ –Є
–Љ–µ–і–Є–∞–љ–∞, –Є
–≤—Л—Б–Њ—В–∞ (–њ–Њ —В—А–µ—В—М–µ–Љ—Г
—Б–≤–Њ–є—Б—В–≤—Г —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞).
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, AO=OD=AD/2=164/2=82.
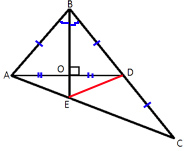 –Я—А–Њ–≤–µ–і–µ–Љ –Њ—В—А–µ–Ј–Њ–Ї ED –Є —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї BEC.
–Я—А–Њ–≤–µ–і–µ–Љ –Њ—В—А–µ–Ј–Њ–Ї ED –Є —А–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї BEC.
ED -
–Љ–µ–і–Є–∞–љ–∞ —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, —В–∞–Ї –Ї–∞–Ї –і–µ–ї–Є—В —Б—В–Њ—А–Њ–љ—Г BC –њ–Њ–њ–Њ–ї–∞–Љ.
–Я–ї–Њ—Й–∞–і–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ EDC –Є EDB —А–∞–≤–љ—Л (–њ–Њ –≤—В–Њ—А–Њ–Љ—Г
—Б–≤–Њ–є—Б—В–≤—Г –Љ–µ–і–Є–∞–љ—Л).
SEDC=SEDB=(BE*OD)/2=(164*82)/2=82*82=6724
SABE=(BE*AO)/2=(164*82)/2=6724
–Ґ.–µ. SABE=SEDC=SEDB=6724
–Ґ–Њ–≥–і–∞, SAB–°=3*6724=20172
AD -
–Љ–µ–і–Є–∞–љ–∞ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC (–њ–Њ —Г—Б–ї–Њ–≤–Є—О), —Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ –і–µ–ї–Є—В —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї –љ–∞ –і–≤–∞ —А–∞–≤–љ—Л—Е –њ–Њ –њ–ї–Њ—Й–∞–і–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABD –Є ACD (–њ–Њ
–≤—В–Њ—А–Њ–Љ—Г —Б–≤–Њ–є—Б—В–≤—Г –Љ–µ–і–Є–∞–љ—Л).
SABD=(AD*BO)/2=SABC/2
(164*BO)/2=20172/2
BO=20172/164=123
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї ABO, –Њ–љ
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–є, —В–Њ–≥–і–∞ –њ—А–Є–Љ–µ–љ–Є–Љ
—В–µ–Њ—А–µ–Љ—Г –Я–Є—Д–∞–≥–Њ—А–∞:
AB2=BO2+AO2
AB2=1232+822
AB2=15129+6724=21853
AB=√
BC=2AB=2*41√
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї AOE.
OE=BE-BO=164-123=41
–Ґ–∞–Ї –Ї–∞–Ї —Н—В–Њ—В —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї —В–Њ–ґ–µ
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л–є, —В–Њ –Љ–Њ–ґ–љ–Њ –њ—А–Є–Љ–µ–љ–Є—В—М
—В–µ–Њ—А–µ–Љ—Г –Я–Є—Д–∞–≥–Њ—А–∞:
AE2=AO2+OE2
AE2=822+412=6724+1681=8405
AE=√
–Ґ–∞–Ї –Ї–∞–Ї BE -
–±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞, —В–Њ –Є—Б–њ–Њ–ї—М–Ј—Г—П –µ–µ
–њ–µ—А–≤–Њ–µ —Б–≤–Њ–є—Б—В–≤–Њ –Ј–∞–њ–Є—И–µ–Љ:
BC/AB=CE/AE
82√
2=CE/(41√
CE=82√
AC=AE+CE=41√
–Ю—В–≤–µ—В: AB=41√
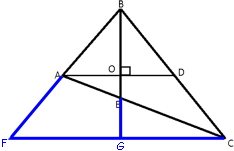 –Я—А–Њ–≤–µ–і—С–Љ —З–µ—А–µ–Ј —В–Њ—З–Ї—Г C –њ—А—П–Љ—Г—О, –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Г—О AD. –Я—А–Њ–і–ї–Є–Љ BA –Є BE –і–Њ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П —Б —Н—В–Њ–є –њ—А—П–Љ–Њ–є –≤ —В–Њ—З–Ї–∞—Е F –Є G —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ.
–Я—А–Њ–≤–µ–і—С–Љ —З–µ—А–µ–Ј —В–Њ—З–Ї—Г C –њ—А—П–Љ—Г—О, –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Г—О AD. –Я—А–Њ–і–ї–Є–Љ BA –Є BE –і–Њ –њ–µ—А–µ—Б–µ—З–µ–љ–Є—П —Б —Н—В–Њ–є –њ—А—П–Љ–Њ–є –≤ —В–Њ—З–Ї–∞—Е F –Є G —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ.–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
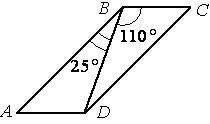 –Ф–Є–∞–≥–Њ–љ–∞–ї—М BD –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –Њ–±—А–∞–Ј—Г–µ—В —Б –µ–≥–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є —Г–≥–ї—Л, —А–∞–≤–љ—Л–µ
25¬∞ –Є 110¬∞. –Э–∞–є–і–Є—В–µ –Љ–µ–љ—М—И–Є–є —Г–≥–Њ–ї –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞.
–Ф–Є–∞–≥–Њ–љ–∞–ї—М BD –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –Њ–±—А–∞–Ј—Г–µ—В —Б –µ–≥–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є —Г–≥–ї—Л, —А–∞–≤–љ—Л–µ
25¬∞ –Є 110¬∞. –Э–∞–є–і–Є—В–µ –Љ–µ–љ—М—И–Є–є —Г–≥–Њ–ї –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞.
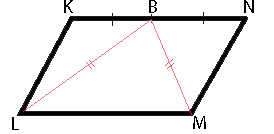 –Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ KLMN —В–Њ—З–Ї–∞ B вАФ —Б–µ—А–µ–і–Є–љ–∞ —Б—В–Њ—А–Њ–љ—Л KN. –Ш–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ BL=BM. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ –і–∞–љ–љ—Л–є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ вАФ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї.
–Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ KLMN —В–Њ—З–Ї–∞ B вАФ —Б–µ—А–µ–і–Є–љ–∞ —Б—В–Њ—А–Њ–љ—Л KN. –Ш–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ BL=BM. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ –і–∞–љ–љ—Л–є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ вАФ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї.
 –†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–∞–њ–µ—Ж–Є—О, —А–∞–≤–µ–љ 24. –Э–∞–є–і–Є—В–µ –≤—Л—Б–Њ—В—Г —Н—В–Њ–є —В—А–∞–њ–µ—Ж–Є–Є.
–†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ —В—А–∞–њ–µ—Ж–Є—О, —А–∞–≤–µ–љ 24. –Э–∞–є–і–Є—В–µ –≤—Л—Б–Њ—В—Г —Н—В–Њ–є —В—А–∞–њ–µ—Ж–Є–Є.
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C –њ—А—П–Љ–Њ–є, AC=6, cosA=0,6. –Э–∞–є–і–Є—В–µ AB.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C –њ—А—П–Љ–Њ–є, AC=6, cosA=0,6. –Э–∞–є–і–Є—В–µ AB.
 –І–µ–ї–Њ–≤–µ–Ї, —А–Њ—Б—В –Ї–Њ—В–Њ—А–Њ–≥–Њ —А–∞–≤–µ–љ 1,6 –Љ, —Б—В–Њ–Є—В –љ–∞ —А–∞—Б—Б—В–Њ—П–љ–Є–Є 17 –Љ –Њ—В —Г–ї–Є—З–љ–Њ–≥–Њ —Д–Њ–љ–∞—А—П. –Я—А–Є —Н—В–Њ–Љ –і–ї–Є–љ–∞ —В–µ–љ–Є —З–µ–ї–Њ–≤–µ–Ї–∞ —А–∞–≤–љ–∞ 8 –Љ. –Ю–њ—А–µ–і–µ–ї–Є—В–µ –≤—Л—Б–Њ—В—Г —Д–Њ–љ–∞—А—П (–≤ –Љ–µ—В—А–∞—Е).
–І–µ–ї–Њ–≤–µ–Ї, —А–Њ—Б—В –Ї–Њ—В–Њ—А–Њ–≥–Њ —А–∞–≤–µ–љ 1,6 –Љ, —Б—В–Њ–Є—В –љ–∞ —А–∞—Б—Б—В–Њ—П–љ–Є–Є 17 –Љ –Њ—В —Г–ї–Є—З–љ–Њ–≥–Њ —Д–Њ–љ–∞—А—П. –Я—А–Є —Н—В–Њ–Љ –і–ї–Є–љ–∞ —В–µ–љ–Є —З–µ–ї–Њ–≤–µ–Ї–∞ —А–∞–≤–љ–∞ 8 –Љ. –Ю–њ—А–µ–і–µ–ї–Є—В–µ –≤—Л—Б–Њ—В—Г —Д–Њ–љ–∞—А—П (–≤ –Љ–µ—В—А–∞—Е).
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є: