В окружности с центром в точке O проведены диаметры AD и BC, угол OAB равен 70°. Найдите величину угла OCD.
Рассмотрим треугольник АОВ. Этот треугольник
равнобедренный, т.к. ОА и ОВ - радиусы, поэтому они равны.
По
свойству равнобедренного треугольника ∠OAB=∠OBA.
Рассмотрим треугольники АОВ и COD. ∠DOC=∠AOB, т.к. они
вертикальные. СО=DO=OB=OA, т.к. это радиусы окружности.
Следовательно, треугольники АОВ и COD равны (по
первому признаку). Поэтому ∠OBA=∠OAB=∠ODC=∠OCD=70°
Ответ: 70
Поделитесь решением
Присоединяйтесь к нам...
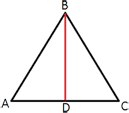Сторона равностороннего треугольника равна 10√
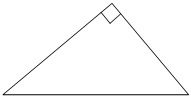Катеты прямоугольного треугольника равны 30 и 40. Найдите гипотенузу этого треугольника.
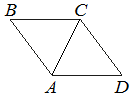В ромбе ABCD угол ABC равен 72°. Найдите угол ACD. Ответ дайте в градусах.
Сколько досок длиной 3,5 м, шириной 20 см и толщиной 10 мм выйдет из бруса длиной 140 дм, имеющего в сечении прямоугольник размером 50 см × 60 см?
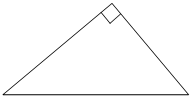Один из острых углов прямоугольного треугольника равен 48°. Найдите его другой острый угол. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: