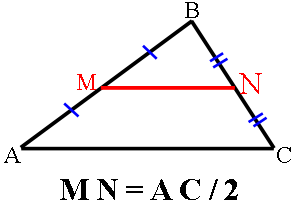
В равнобедренном треугольнике ABC (АВ=ВС) точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равнобедренный.
NK - является
средней линией треугольника ABC и равна половине AB.
MK - является
средней линией треугольника ABC и равна половине BC.
Т.к. AB=BC (по условию), то NK=MK.
Следовательно треугольник MNK -
равнобедренный.
Поделитесь решением
Присоединяйтесь к нам...
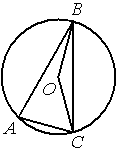Точка О – центр окружности, /BAC=75° (см. рисунок). Найдите величину угла BOC (в градусах).
Радиус вписанной в квадрат окружности равен 14√
Сторона AC треугольника ABC проходит через центр окружности. Найдите
∠C, если ∠A=83°. Ответ дайте в градусах.
Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит больший угол.
2) Любой прямоугольник можно вписать в окружность.
3) Площадь треугольника меньше произведения двух его сторон.
Синус острого угла A треугольника ABC равен √
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: