
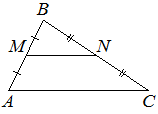
 Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 48, сторона BC равна 57, сторона AC равна 72. Найдите MN.
Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 48, сторона BC равна 57, сторона AC равна 72. Найдите MN.
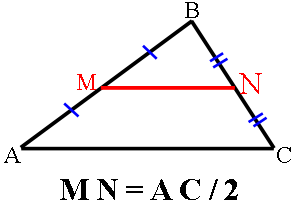
MN -
средняя треугольника по определению.
Тогда, по теореме о средней линии:
MN=AC/2=72/2=36
Ответ: 36
Поделитесь решением
Присоединяйтесь к нам...
 Катеты прямоугольного треугольника равны 2√
Катеты прямоугольного треугольника равны 2√
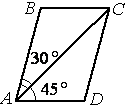 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
В параллелограмме KLMN точка A — середина стороны LM. Известно, что KA=NA. Докажите, что данный параллелограмм — прямоугольник.
 Площадь прямоугольного треугольника равна 98√
Площадь прямоугольного треугольника равна 98√
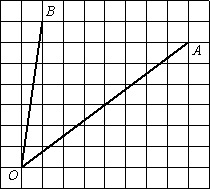 Найдите тангенс угла AOB.
Найдите тангенс угла AOB.
Комментарии: