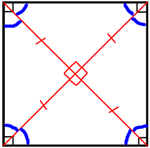
Найдите площадь квадрата, если его диагональ равна 1.
По
определению стороны
квадрата равны друг другу, обозначим длину сторон как "а".
По
свойству, все углы квадрата прямые, следовательно можно применить
теорему Пифагора для получившегося треугольника, квадрат диагонали будет равен сумме квадратов сторон:
a2+a2=12
2a2=1
a2=0,5
a2 - это и есть площадь квадрата.
Ответ: 0,5
Поделитесь решением
Присоединяйтесь к нам...
Сторона ромба равна 8, а расстояние от точки пересечения диагоналей ромба до неё равно 2. Найдите площадь этого ромба.
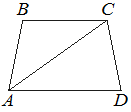Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 46° и 1° соответственно. Ответ дайте в градусах.
В треугольнике ABC угол C равен 90°, sinA=0,4, AC=√
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.
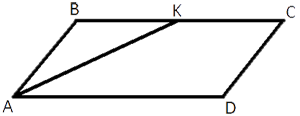Сторона BC параллелограмма ABCD вдвое больше стороны AB.
Точка K — середина стороны BC. Докажите, что AK — биссектриса
угла BAD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: