Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
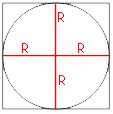Стороны
квадрата являются
касательными к окружности, следовательно, отрезок, проведенный от центра окружности к точке касания будет перпендикулярен стороне
квадрата и равен радиусу окружности (По
свойству касательной).
Получается, что сторона
квадрата равна диаметру окружности, или двум радиусам, т.е. 2*83=166
Площадь
квадрата равна произведению сторон:
S=166*166=27556
Ответ: 27556
Поделитесь решением
Присоединяйтесь к нам...
Сколько досок длиной 3,5 м, шириной 20 см и толщиной 10 мм выйдет из бруса длиной 140 дм, имеющего в сечении прямоугольник размером 50 см × 60 см?
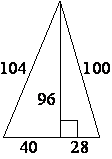Найдите площадь треугольника, изображённого на рисунке.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 66°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
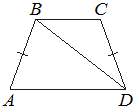
Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и ADB подобны.
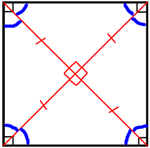
В трапеции ABCD известно, что AB=CD, ∠BDA=38° и ∠BDC=32°. Найдите угол ABD. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: