
 –ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α
–ê–≤―²–Ψ―Ä: –Δ–Α―¹―¨–Κ–Α–½–Α–¥–Α―΅–Α ⳕ930 –Η–Ζ 1087 |
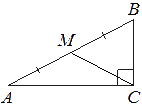 –£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC ―É–≥–Ψ–Μ C ―Ä–Α–≤–Β–Ϋ 90¬Α, M βÄî ―¹–Β―Ä–Β–¥–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB, AB=20, BC=10. –ù–Α–Ι–¥–Η―²–Β CM.
–£ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β ABC ―É–≥–Ψ–Μ C ―Ä–Α–≤–Β–Ϋ 90¬Α, M βÄî ―¹–Β―Ä–Β–¥–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB, AB=20, BC=10. –ù–Α–Ι–¥–Η―²–Β CM.
–ü–Β―Ä–≤―΄–Ι –≤–Α―Ä–Η–Α–Ϋ―² ―Ä–Β―à–Β–Ϋ–Η―è
 –Δ–Α–Κ –Κ–Α–Κ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ABC –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ―΄–Ι, ―²–Ψ –≤–Ψ―¹–Ω–Ψ–Μ―¨–Ζ―É–Β–Φ―¹―è ―²–Β–Ψ―Ä–Β–Φ–Ψ–Ι –Ψ–± –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η –¥–Μ―è –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α. –î–Μ―è ―ç―²–Ψ–≥–Ψ –Ψ–Ω–Η―à–Β–Φ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨ –≤–Ψ–Κ―Ä―É–≥ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC.
–Δ–Α–Κ –Κ–Α–Κ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ ABC –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ―΄–Ι, ―²–Ψ –≤–Ψ―¹–Ω–Ψ–Μ―¨–Ζ―É–Β–Φ―¹―è ―²–Β–Ψ―Ä–Β–Φ–Ψ–Ι –Ψ–± –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η –¥–Μ―è –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α. –î–Μ―è ―ç―²–Ψ–≥–Ψ –Ψ–Ω–Η―à–Β–Φ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²―¨ –≤–Ψ–Κ―Ä―É–≥ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ABC.
–Π–Β–Ϋ―²―Ä –Ψ–Ω–Η―¹–Α–Ϋ–Ϋ–Ψ–Ι –≤–Ψ–Κ―Ä―É–≥ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–≥–Ψ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η –Μ–Β–Ε–Η―² –Ϋ–Α ―¹–Β―Ä–Β–¥–Η–Ϋ–Β –≥–Η–Ω–Ψ―²–Β–Ϋ―É–Ζ―΄.
–ü–Ψ–Μ―É―΅–Α–Β―²―¹―è, ―΅―²–Ψ ―²–Ψ―΅–Κ–Α –€ –Η –Β―¹―²―¨ ―Ü–Β–Ϋ―²―Ä –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¨–Ϋ–Ψ:
R=AM=MB=AB/2=20/2=10
CM ―²–Ψ–Ε–Β ―è–≤–Μ―è–Β―²―¹―è ―Ä–Α–¥–Η―É―¹–Ψ–Φ –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, ―².–Β.:
CM=R=10
–û―²–≤–Β―²: 10
–ü–Ψ–¥–Β–Μ–Η―²–Β―¹―¨ ―Ä–Β―à–Β–Ϋ–Η–Β–Φ
–ü―Ä–Η―¹–Ψ–Β–¥–Η–Ϋ―è–Ι―²–Β―¹―¨ –Κ –Ϋ–Α–Φ...
 –Δ–Ψ―΅–Κ–Α –û βÄ™ ―Ü–Β–Ϋ―²―Ä –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, /ACB=25¬Α (―¹–Φ. ―Ä–Η―¹―É–Ϋ–Ψ–Κ). –ù–Α–Ι–¥–Η―²–Β –≤–Β–Μ–Η―΅–Η–Ϋ―É ―É–≥–Μ–Α AOB (–≤ –≥―Ä–Α–¥―É―¹–Α―Ö).
–Δ–Ψ―΅–Κ–Α –û βÄ™ ―Ü–Β–Ϋ―²―Ä –Ψ–Κ―Ä―É–Ε–Ϋ–Ψ―¹―²–Η, /ACB=25¬Α (―¹–Φ. ―Ä–Η―¹―É–Ϋ–Ψ–Κ). –ù–Α–Ι–¥–Η―²–Β –≤–Β–Μ–Η―΅–Η–Ϋ―É ―É–≥–Μ–Α AOB (–≤ –≥―Ä–Α–¥―É―¹–Α―Ö).
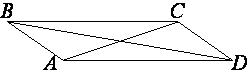 –£ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Β ABCD –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―¨ AC –≤ 2 ―Ä–Α–Ζ–Α –±–Ψ–Μ―¨―à–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB –Η ∠ACD=169¬Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ –Φ–Β–Ε–¥―É –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―è–Φ–Η –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
–£ –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Β ABCD –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―¨ AC –≤ 2 ―Ä–Α–Ζ–Α –±–Ψ–Μ―¨―à–Β ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ AB –Η ∠ACD=169¬Α. –ù–Α–Ι–¥–Η―²–Β ―É–≥–Ψ–Μ –Φ–Β–Ε–¥―É –¥–Η–Α–≥–Ψ–Ϋ–Α–Μ―è–Φ–Η –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α. –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ –≥―Ä–Α–¥―É―¹–Α―Ö.
 –ö–Α―Ä―²–Η–Ϋ–Κ–Α –Η–Φ–Β–Β―² ―³–Ψ―Ä–Φ―É –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―¹–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ–Α–Φ–Η 24 ―¹–Φ –Η 37 ―¹–Φ. –ï―ë –Ϋ–Α–Κ–Μ–Β–Η–Μ–Η –Ϋ–Α –±–Β–Μ―É―é –±―É–Φ–Α–≥―É ―²–Α–Κ, ―΅―²–Ψ –≤–Ψ–Κ―Ä―É–≥ –Κ–Α―Ä―²–Η–Ϋ–Κ–Η –Ω–Ψ–Μ―É―΅–Η–Μ–Α―¹―¨ –±–Β–Μ–Α―è –Ψ–Κ–Α–Ϋ―²–Ψ–≤–Κ–Α –Ψ–¥–Η–Ϋ–Α–Κ–Ψ–≤–Ψ–Ι ―à–Η―Ä–Η–Ϋ―΄. –ü–Μ–Ψ―â–Α–¥―¨, –Κ–Ψ―²–Ψ―Ä―É―é –Ζ–Α–Ϋ–Η–Φ–Α–Β―² –Κ–Α―Ä―²–Η–Ϋ–Κ–Α ―¹ –Ψ–Κ–Α–Ϋ―²–Ψ–≤–Κ–Ψ–Ι, ―Ä–Α–≤–Ϋ–Α 1440 ―¹–Φ2. –ö–Α–Κ–Ψ–≤–Α ―à–Η―Ä–Η–Ϋ–Α –Ψ–Κ–Α–Ϋ―²–Ψ–≤–Κ–Η? –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ ―¹–Α–Ϋ―²–Η–Φ–Β―²―Ä–Α―Ö.
–ö–Α―Ä―²–Η–Ϋ–Κ–Α –Η–Φ–Β–Β―² ―³–Ψ―Ä–Φ―É –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Α ―¹–Ψ ―¹―²–Ψ―Ä–Ψ–Ϋ–Α–Φ–Η 24 ―¹–Φ –Η 37 ―¹–Φ. –ï―ë –Ϋ–Α–Κ–Μ–Β–Η–Μ–Η –Ϋ–Α –±–Β–Μ―É―é –±―É–Φ–Α–≥―É ―²–Α–Κ, ―΅―²–Ψ –≤–Ψ–Κ―Ä―É–≥ –Κ–Α―Ä―²–Η–Ϋ–Κ–Η –Ω–Ψ–Μ―É―΅–Η–Μ–Α―¹―¨ –±–Β–Μ–Α―è –Ψ–Κ–Α–Ϋ―²–Ψ–≤–Κ–Α –Ψ–¥–Η–Ϋ–Α–Κ–Ψ–≤–Ψ–Ι ―à–Η―Ä–Η–Ϋ―΄. –ü–Μ–Ψ―â–Α–¥―¨, –Κ–Ψ―²–Ψ―Ä―É―é –Ζ–Α–Ϋ–Η–Φ–Α–Β―² –Κ–Α―Ä―²–Η–Ϋ–Κ–Α ―¹ –Ψ–Κ–Α–Ϋ―²–Ψ–≤–Κ–Ψ–Ι, ―Ä–Α–≤–Ϋ–Α 1440 ―¹–Φ2. –ö–Α–Κ–Ψ–≤–Α ―à–Η―Ä–Η–Ϋ–Α –Ψ–Κ–Α–Ϋ―²–Ψ–≤–Κ–Η? –û―²–≤–Β―² –¥–Α–Ι―²–Β –≤ ―¹–Α–Ϋ―²–Η–Φ–Β―²―Ä–Α―Ö.
 –ù–Α–Ι–¥–Η―²–Β –±–Ψ–Κ–Ψ–≤―É―é ―¹―²–Ψ―Ä–Ψ–Ϋ―É AB ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD, –Β―¹–Μ–Η ―É–≥–Μ―΄ ABC –Η BCD ―Ä–Α–≤–Ϋ―΄ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ 45¬Α –Η 120¬Α, –Α CD=34.
–ù–Α–Ι–¥–Η―²–Β –±–Ψ–Κ–Ψ–≤―É―é ―¹―²–Ψ―Ä–Ψ–Ϋ―É AB ―²―Ä–Α–Ω–Β―Ü–Η–Η ABCD, –Β―¹–Μ–Η ―É–≥–Μ―΄ ABC –Η BCD ―Ä–Α–≤–Ϋ―΄ ―¹–Ψ–Ψ―²–≤–Β―²―¹―²–≤–Β–Ϋ–Ϋ–Ψ 45¬Α –Η 120¬Α, –Α CD=34.
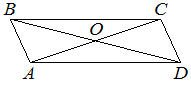 –î–Η–Α–≥–Ψ–Ϋ–Α–Μ–Η AC –Η BD –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ABCD –Ω–Β―Ä–Β―¹–Β–Κ–Α―é―²―¹―è –≤ ―²–Ψ―΅–Κ–Β O, AC=12, BD=20, AB=7. –ù–Α–Ι–¥–Η―²–Β DO.
–î–Η–Α–≥–Ψ–Ϋ–Α–Μ–Η AC –Η BD –Ω–Α―Ä–Α–Μ–Μ–Β–Μ–Ψ–≥―Ä–Α–Φ–Φ–Α ABCD –Ω–Β―Ä–Β―¹–Β–Κ–Α―é―²―¹―è –≤ ―²–Ψ―΅–Κ–Β O, AC=12, BD=20, AB=7. –ù–Α–Ι–¥–Η―²–Β DO.
–ö–Ψ–Φ–Φ–Β–Ϋ―²–Α―Ä–Η–Η:
(2021-10-17 20:32:36) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –ï–Μ–Β–Ϋ–Α, –Ζ–¥―Ä–Α–≤―¹―²–≤―É–Ι―²–Β. –£–Η–¥–Η–Φ–Ψ, ―É―¹–Μ–Ψ–≤–Η–Β - ―ç―²–Ψ ―à–Α–±–Μ–Ψ–Ϋ –¥–Μ―è ―¹–Ψ―¹―²–Α–≤–Μ–Β–Ϋ–Η―è ―Ü–Β–Μ–Ψ–Ι ―¹–Β―Ä–Η–Η –Ζ–Α–¥–Α―΅ ―¹ ―Ä–Α–Ζ–Ϋ―΄–Φ–Η –≤–Ψ–Ω―Ä–Ψ―¹–Α–Φ–Η. –£ –¥–Α–Ϋ–Ϋ–Ψ–Φ ―¹–Μ―É―΅–Α–Β –¥–Μ–Η–Ϋ–Α –Κ–Α―²–Β―²–Α –Ϋ–Β –Ω―Ä–Η–≥–Ψ–¥–Η–Μ–Α―¹―¨, –≤ –¥―Ä―É–≥–Ψ–Φ, –≤–Ψ–Ζ–Φ–Ψ–Ε–Ϋ–Ψ, –Ω–Ψ–Ϋ–Α–¥–Ψ–±–Η―²―¹―è...
(2021-10-17 06:52:52) –ï–Μ–Β–Ϋ–Α: –½–¥―Ä–Α–≤―¹―²–≤―É–Ι―²–Β. –½–Α―΅–Β–Φ –¥–Α–Ϋ–Α –¥–Μ–Η–Ϋ–Α –Κ–Α―²–Β―²–Α?
(2021-10-14 18:20:28) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –î–Β–Ϋ–Η―¹, ―¹–Ψ–≥–Μ–Α―¹–Β–Ϋ ―¹ –≤–Α–Φ–Η, –¥–Ψ–±–Α–≤–Η–Μ –≤–Α―à –≤–Α―Ä–Η–Α–Ϋ―².
(2021-03-25 20:57:33) –î–Β–Ϋ–Η―¹.: –½–Α―΅–Β–Φ –≤―¹―ë ―²–Α–Κ ―É―¹–Μ–Ψ–Ε–Ϋ―è―²―¨?–ù–Β –Μ–Β–≥―΅–Β –Ω―Ä–Ψ―¹―²–Ψ –≤–Ψ―¹–Ω–Ψ–Μ―¨–Ζ–Ψ–≤–Α―²―¨―¹―è –Ω―Ä–Α–≤–Η–Μ–Ψ–Φ ,―²–Ψ ―΅―²–Ψ –≤ –Ω―Ä―è–Φ–Ψ―É–≥–Ψ–Μ―¨–Ϋ–Ψ–Φ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β –Φ–Β–¥–Η–Α–Ϋ–Α –Ω―Ä–Ψ–≤–Β–¥–Β–Ϋ–Ϋ–Α―è –Κ –≥–Η–Ω–Ψ―²–Β–Ϋ―É–Ζ–Β ―Ä–Α–≤–Ϋ–Α –Ω–Ψ–Μ–Ψ–≤–Η–Ϋ–Β –≥–Η–Ω–Ψ―²–Β–Ϋ―É–Ζ―΄
(2020-04-15 11:20:54) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –ê–Μ–Β–Κ―¹–Α–Ϋ–¥―Ä–Α, –€―΄ –Ϋ–Β –Ω–Ψ–Φ–Ψ–≥–Α–Β–Φ ―Ä–Β―à–Η―²―¨ –¥–Ψ–Φ–Α―à–Ϋ–Β–Β –Ζ–Α–¥–Α–Ϋ–Η–Β, ―Ü–Β–Μ―¨ ―¹–Α–Ι―²–Α - –Ω–Ψ–¥―Ä–Ψ–±–Ϋ–Ψ ―Ä–Α–Ζ–Ψ–±―Ä–Α―²―¨ –Ζ–Α–¥–Α―΅–Η, –Κ–Ψ―²–Ψ―Ä―΄–Β –±―É–¥―É―² –Ϋ–Α ―ç–Κ–Ζ–Α–Φ–Β–Ϋ–Α―Ö, ―΅―²–Ψ–±―΄ ―É―΅–Α―â–Η–Β―¹―è –Ϋ–Α―É―΅–Η–Μ–Η―¹―¨ –Η―Ö ―Ä–Β―à–Α―²―¨ ―¹–Α–Φ–Ψ―¹―²–Ψ―è―²–Β–Μ―¨–Ϋ–Ψ. –ï―¹–Μ–Η –Ϋ–Α–Ι–¥–Β―²–Β –Ω–Ψ―Ö–Ψ–Ε―É―é –Ζ–Α–¥–Α―΅―É –Ϋ–Α ―¹–Α–Ι―²–Β fipi.ru, –Ψ―²–Ω―Ä–Α–≤―¨―²–Β –Ζ–Α―è–≤–Κ―É –Ϋ–Α –¥–Ψ–±–Α–≤–Μ–Β–Ϋ–Η–Β –Ζ–Α–¥–Α―΅–Η, –Η –Φ―΄ –Β–Β –Ψ–±―è–Ζ–Α―²–Β–Μ―¨–Ϋ–Ψ –¥–Ψ–±–Α–≤–Η–Φ.
(2020-04-12 19:50:28) –ê–Μ–Β–Κ―¹–Α–Ϋ–¥―Ä–Α: –≤ ―²―Ä–Β―É–≥–Ψ–Μ―¨–Ϋ–Η–Κ–Β –Α–≤―¹ ―É–≥–Ψ–Μ ―¹ ―Ä–Α–≤–Β–Ϋ 90 –€- ―¹–Β―Ä–Β–¥–Η–Ϋ–Α ―¹―²–Ψ―Ä–Ψ–Ϋ―΄ –Α–≤, –Α–≤=64 –≤―¹=44 –Ϋ–Α–Ι―²–Η ―¹–Φ
(2019-03-22 18:27:58) –ê–¥–Φ–Η–Ϋ–Η―¹―²―Ä–Α―²–Ψ―Ä: –€–Η―à–Α, ―Ä–Β―à–Β–Ϋ–Η–Β –Ω–Β―Ä–Β–¥ –≤–Α–Φ–Η, ―É―²–Ψ―΅–Ϋ–Η―²–Β, –Ω–Ψ–Ε–Α–Μ―É–Ι―¹―²–Α, –≤–Ψ–Ω―Ä–Ψ―¹.
(2019-03-20 23:29:13) –Φ–Η―à–Α: –Α –Ω–Ψ―΅–Β–Φ―É –≤ –Ψ―²–≤–Β―²–Β 10