В треугольнике ABC известны длины сторон AB=30, AC=100, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D.
Найдите CD.
Проведем дополнительный отрезок и введем обозначения как показано на рисунке:
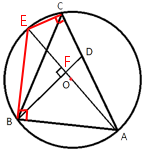Рассмотрим треугольники AEB и AFB.
∠BAE - общий
Треугольник AEB - прямоугольный, т.к. центр окружности лежит на стороне этого треугольника (
теорема об описанной окружности)
Т.е. ∠EBA=90°
∠AFB=90°, т.к. по условию AD ⊥ AE
Следовательно, по
первому признаку подобия треугольников, данные треугольники
подобны.
Тогда:
AE/AB=AB/AF => AE*AF=AB2
Рассмотрим треугольники AEC и AFD.
∠FAD - общий
∠ACE=90°, т.к. AE - диаметр окружности (
теорема об описанной окружности)
∠AFD=90°, т.к. по условию BD ⊥ AE
Следовательно, по
первому признаку подобия треугольников, данные треугольники
подобны.
Тогда:
AE/AD=AC/AF => AD=AE*AF/AC
Подставляем выше найденное равенство:
AD=AB2/AC=302/100=9
CD=AC-AD=100-9=91
Ответ: 91
Поделитесь решением
Присоединяйтесь к нам...
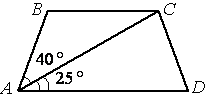Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 25° и 40° соответственно.
Укажите номера верных утверждений.
1) Центр вписанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Ромб не является параллелограммом.
3) Сумма острых углов прямоугольного треугольника равна 90°.
Боковые стороны AB и CD трапеции ABCD равны соответственно 12 и 15, а основание BC равно 3. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
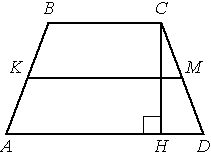В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 6.
В трапеции ABCD основания AD и BC равны соответственно 48 и 3, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=3.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2020-05-05 17:14:49) Администратор: Влад, это не бред, а опечатка. Исправлено!
(2020-05-05 16:53:07) Влад: че за бред? как отрезки, лежащие на одной стороне могут быть перпендикулярны?!?!?!