
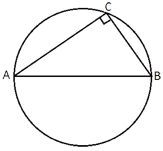
 В треугольнике ABC AC=15, BC=5√
В треугольнике ABC AC=15, BC=5√
Треугольник ABC -
прямоугольный, тогда по
теореме Пифагора:
AB2=AC2+BC2
AB2=152+(5√
AB2=225+25*7
AB2=400
AB=20
Так как треугольник ABC прямоугольный, то это означает, что центр окружности находится на середине гипотенузы (по
теореме об описанной окружности).
Тогда R=AB/2=20/2=10
Ответ: R=10
Поделитесь решением
Присоединяйтесь к нам...
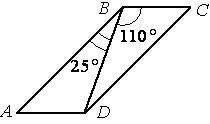 Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
25° и 110°. Найдите меньший угол параллелограмма.
Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
25° и 110°. Найдите меньший угол параллелограмма.
 Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 16, а площадь равна 32√
Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 16, а площадь равна 32√
Укажите номера верных утверждений.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Синус острого угла A треугольника ABC равен 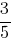 . Найдите CosA.
. Найдите CosA.
Комментарии: